题目内容
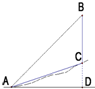 如图,在坡角为15°(∠CAD=15°)的山坡顶上有一个高度为50米的中国移动信号塔BC,在坡底A处测得塔顶B的仰角为45°(∠BAD=45°),则塔顶到水平面AD的距离(BD)约为
如图,在坡角为15°(∠CAD=15°)的山坡顶上有一个高度为50米的中国移动信号塔BC,在坡底A处测得塔顶B的仰角为45°(∠BAD=45°),则塔顶到水平面AD的距离(BD)约为| 3 |
考点:解三角形的实际应用
专题:解三角形
分析:先求得∠BAD进而由正弦定理求得AC,最后求得sin15°的值,通过CD=AC•sin15°求得CD,最后把CD与BC相加.
解答:
解:依题意知∠BAD=45°-15°=30°,
=
,
∴AC=
=
=50
,
CD=AC•sin15°=ACsin(45°-30°)=AC•(
×
-
×
)=25(
-1)=18.2(米)≈18米,
∴BD=BC+CD=50+18=68米,
即塔顶到水平面AD的距离为68米.
故答案为:68.
| BC |
| sin∠BAD |
| AC |
| sinB |
∴AC=
| BC•sinB |
| sin∠BAD |
50×
| ||||
|
| 2 |
CD=AC•sin15°=ACsin(45°-30°)=AC•(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴BD=BC+CD=50+18=68米,
即塔顶到水平面AD的距离为68米.
故答案为:68.
点评:本题主要考查了正弦定理的应用.考查了学生运用所学解决实际问题的能力.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
已知i为虚数单位,a∈R,若(a-1)(a+1+i)=a2-1+(a-1)i是纯虚数,则a的值为( )
| A、-1或1 | B、1 | C、3 | D、-1 |
