题目内容
9.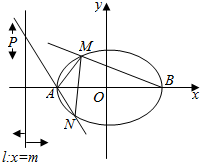 已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.
已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.(1)求椭圆C的方程;
(2)设A、B分别是椭圆C的左、右顶点,直线l:x=m(m≠2),当点P在直线l(纵坐标不为0)上移动时,直线PB、线段PA的延长线与椭圆C分别相交于M、N两点,且以MN为直径的圆恒经过点A,求m的值.
分析 (1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),可得$e=\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,b=1,a2=b2+c2,联立解出即可得出;
(2)设P(m,yP),A(-2,0),B(2,0),N(x1,y1),M(x2,y2).由于以MN为直径的圆恒经过点A,不妨设直线AM、AN的方程为:ky=x+2,-$\frac{1}{k}$y=x+2,k≠0.联立$\left\{\begin{array}{l}{ky=x+2}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,解得M坐标.可得直线BM的方程,令x=m,解得yP.由直线AN的方程,令x=m,解得yP,进而解出m.
解答 解:(1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),∵$e=\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,b=1,a2=b2+c2,
解得b=1,a=2,c=$\sqrt{3}$.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)设P(m,yP),A(-2,0),B(2,0),N(x1,y1),M(x2,y2).
∵以MN为直径的圆恒经过点A,
∴不妨设直线AM、AN的方程为:ky=x+2,-$\frac{1}{k}$y=x+2,k≠0.
联立$\left\{\begin{array}{l}{ky=x+2}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,
化为:(k2+4)y2-4ky=0,
解得yM=$\frac{4k}{{k}^{2}+4}$,xM=kyM-2=$\frac{2{k}^{2}-8}{{k}^{2}+4}$.
直线BM的方程为:y=$\frac{\frac{4k}{{k}^{2}+4}}{\frac{2{k}^{2}-8}{{k}^{2}+4}-2}$(x-2),化为y=-$\frac{k}{4}$(x-2),
令x=m,解得yP=$\frac{-k(m-2)}{4}$.
由-$\frac{1}{k}$y=x+2,令x=m,解得yP=k(m+2).
∴$\frac{-k(m-2)}{4}$=-k(m+2),k≠0.
解得m=$-\frac{10}{3}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、圆的性质、直线方程,考查了数形结合方法、推理能力与计算能力,属于难题.

| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| A. | -4 | B. | -3 | C. | 4 | D. | 3 |