题目内容
1.已知圆C的参数方程为$\left\{\begin{array}{l}{x=2+cosα}\\{y=2\sqrt{3}+sinα}\end{array}\right.$(α为参数).(1)在直角坐标系xOy中,以原点为极点,x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(2)已知A(0,-2)、B(2,0),M为圆C上任意一点,求△ABM面积的最大值.
分析 (1)直接根据圆的参数方程,得到其普通方程,然后,化为极坐标方程即可;
(2)首先,写出直线AB的方程,然后,判断该直线与圆的位置关系,然后,构造面积关系式,求解其最大值.
解答 解:(1)根据圆C的参数方程为$\left\{\begin{array}{l}{x=2+cosα}\\{y=2\sqrt{3}+sinα}\end{array}\right.$(α为参数)得
(x-2)2+(y-2$\sqrt{3}$)2=1,
∴该圆的普通方程为:(x-2)2+(y-2$\sqrt{3}$)2=1,
∴x2+y2-4x-4$\sqrt{3}$y+15=0,
∴ρ2-4ρcosθ-4$\sqrt{3}$ρsinθ+15=0,
∴圆C的极坐标方程:ρ2-4ρcosθ-4$\sqrt{3}$ρsinθ+15=0,
(2)∵A(0,-2)、B(2,0),
∴直线AB的方程为:$\frac{x}{2}-\frac{y}{2}=1$,
∴x-y-2=0,
圆心到直线的距离d=$\frac{|2-2\sqrt{3}-2|}{\sqrt{1+(-1)^{2}}}$=$\sqrt{6}$>1,
∴直线AB与圆相离,
∵|AB|=$\sqrt{(0-2)^{2}+(-2-0)^{2}}=2\sqrt{2}$,
∴S△ABM=$\frac{1}{2}$|AB|×d(d为点M到直线的距离),
当d取$\sqrt{6}$+1时,此时所求面积最大,
最大面积为2$\sqrt{3}$+$\sqrt{2}$.
点评 本题重点考查了直线与圆的位置关系、三角形的面积公式、点到直线的距离等知识,属于中档题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,若输出的p是720,则输入的N的值是( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
10.执行如图所示的程序框图,若输出的a等于341,则判断框内应填写( )
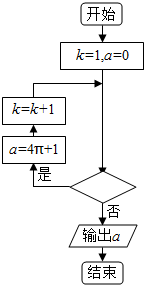

| A. | k<4? | B. | k<5? | C. | k<6? | D. | k<7? |
11.一个人将编号为1,2,3,4的四个小球随机放入编号为1,2,3,4的四个盒子中,每个盒子放一个小球,球的编号与盒子的编号相同时叫做放对了,否则叫做错了,设放对的个数为ξ,则ξ的期望值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
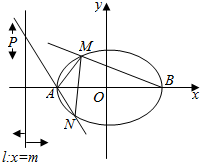 已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.
已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.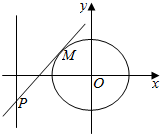 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.