题目内容
已知cos(θ+
)=-
,求
+
的值.
| π |
| 2 |
| 1 |
| 2 |
| cos(θ+π) | ||
sin(
|
| cos(θ-2π) | ||
cos(-θ)•cos(π-θ)+sin(θ+
|
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:先利用诱导公式求得sinθ,在利用诱导公式对原式进行化简整理,最后把sinθ的值代入即可.
解答:
解:∵cos(θ+
)=-
,
∴sinθ=
,
原式=
+
=
+
=
=8.
| π |
| 2 |
| 1 |
| 2 |
∴sinθ=
| 1 |
| 2 |
原式=
| -cosθ |
| cosθ(-cosθ-1) |
| cosθ |
| cosθ•(-cosθ)+cosθ |
| 1 |
| 1+cosθ |
| 1 |
| 1-cosθ |
| 2 |
| sin2θ |
点评:本题主要考查了三角函数恒等变换的应用,诱导公式的化简求值.运用诱导公式时,判断三角函数符号是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知等比数列{an}中,a4=7,a6=21,则a8的值( )
| A、35 | ||
| B、63 | ||
C、21
| ||
D、±21
|
把一个周长为12的长方形卷成一个圆柱,当圆柱的体积最大时,该圆柱的底面周长与高的比为( )
| A、1:2 | B、1:π |
| C、2:1 | D、2:π |
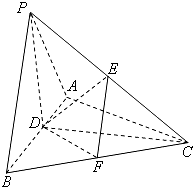 如图,在三棱锥P-ABC中,△PAB是等边三角形,D、E分别为AB、PC的中点.
如图,在三棱锥P-ABC中,△PAB是等边三角形,D、E分别为AB、PC的中点.