题目内容
16.$cos\sqrt{2},sin\sqrt{2},tan\sqrt{2}$的大小关系是( )| A. | $sin\sqrt{2}<cos\sqrt{2}<tan\sqrt{2}$ | B. | $cos\sqrt{2}<sin\sqrt{2}<tan\sqrt{2}$ | C. | $cos\sqrt{2}<tan\sqrt{2}<sin\sqrt{2}$ | D. | $sin\sqrt{2}<tan\sqrt{2}<cos\sqrt{2}$ |
分析 根据$\frac{π}{4}$<$\sqrt{2}$<$\frac{π}{2}$,结合正弦、余弦、正切函数在第一象限内的单调性,
即可得出cos$\sqrt{2}$、sin$\sqrt{2}$和tan$\sqrt{2}$的大小.
解答 解:∵$\frac{π}{4}$<$\sqrt{2}$<$\frac{π}{2}$,
∴cos$\sqrt{2}$<sin$\sqrt{2}$<tan$\sqrt{2}$.
故选:B.
点评 本题考查了正弦、余弦、正切函数在第一象限内的单调性问题,是基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
1.下列四个结论,正确的是( )
①a>b,c<d⇒a-c>b-d
②a>b>0,c<d<0⇒ac>bd
③a>b>0⇒$\root{3}{a}$>$\root{3}{b}$
④a>b>0⇒$\frac{1}{{a}^{2}}$>$\frac{1}{{b}^{2}}$.
①a>b,c<d⇒a-c>b-d
②a>b>0,c<d<0⇒ac>bd
③a>b>0⇒$\root{3}{a}$>$\root{3}{b}$
④a>b>0⇒$\frac{1}{{a}^{2}}$>$\frac{1}{{b}^{2}}$.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
6.已知命题p:?x∈R,x2+2ax+a≤0.若命题p是假命题,则实数a的取值范围是( )
| A. | a<0或a>1 | B. | a≤0或a≥1 | C. | 0≤a≤1 | D. | 0<a<1 |
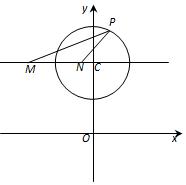 已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0
已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0