题目内容
20.已知△ABC三个顶点坐标分别为A(0,0),B(4,0),C(0,3),点P是△ABC内切圆上一点.(1)求△ABC内切圆的方程;
(2)求以PA、PB、PC为直径的三个圆的面积之和的最大值和最小值.
分析 (1)由已知得AB⊥AC,AB=4,AC=3,BC=5,由此求出△ABC内切圆的半径和圆心,由此能求出△ABC内切圆的方程.
(2)三个圆面积之和的最值问题实质上是求|PA|2+|PB|2+|PC|2的最值,由于P是△ABC内切圆上的点,若想找P点坐标必须先从△ABC内切圆的方程入手.
解答 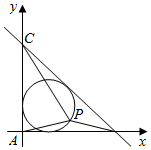 解:(1)∵△ABC三个顶点坐标分别为A(0,0),B(4,0),C(0,3)
解:(1)∵△ABC三个顶点坐标分别为A(0,0),B(4,0),C(0,3)
∴AB⊥AC,AB=4,AC=3,BC=$\sqrt{16+9}$=5,
∴△ABC内切圆的半径r=$\frac{3+4-5}{2}$=1,圆心(1,1),
∴△ABC内切圆的方程为(x-1)2+(y-1)2=1.
(2)设P(x,y),由△ABC的内切圆方程(x-1)2+(y-1)2=1,得x2+y2-2x-2y+1=0.①
|PA|2+|PB|2+|PC|2
=(x-4)2+y2+x2+(y-3)2+x2+y2
=3x2+3y2-8x-6y+25,②
由①知x2+y2-2y=2x-1,
将其代入②,有|PA|2+|PB|2+|PC|2=3(2x-1)-8x+25=-2x+22,
∵x∈[0,2],∴|PA|2+|PB|2+|PC|2的最大值为22,最小值为18,
以PA、PB、PC为直径的三个圆的面积之和:
S=$π(\frac{|PA|}{2})^{2}$+$π(\frac{|PB|}{2})^{2}$+$π(\frac{|PC|}{2})^{2}$
=$\frac{π}{4}$(|PA|2+|PB|2+|PC|2),
∴以PA、PB、PC为直径的三个圆的面积之和的最大值为$\frac{11π}{2}$,最小值为$\frac{9π}{2}$.
点评 本题考查三角形内切圆方程的求法,考查三个圆的面积之和的最值的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

 寒假学与练系列答案
寒假学与练系列答案| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{15}}{3}$ | C. | $\frac{3\sqrt{5}}{4}$ | D. | $\frac{\sqrt{15}}{6}$ |
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<c<b |
| A. | 若z是复数,则|z|2=z2 | |
| B. | 任意两个复数不能比较大小 | |
| C. | 当b2-4ac>0时,一元二次方程ax2+bx+c=0(a、b、c∈C)有两个不相等的实数根 | |
| D. | 在复平面xOy上,复数z=m2+mi(m∈R,i是虚数单位)对应的点的轨迹方程是y2=x |