题目内容
5.设等差数列{an}的前n项和为Sn,且满足a8>0,a8+a9<0,则Sn>0的最大n是15;数列{$\frac{{S}_{n}}{{a}_{n}}$}(1≤n≤15)中最大的项为第8项.分析 直接由已知结合等差数列的性质与前n项和得S15>0,S16<0,则答案可求,
由题意可知,该数列是递减数列,当n=8时,|a8|最小,且|S8|最大,问题得以解决.
解答 解:∵等差数列{an}满足a8>0,a8+a9<0,
∴S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=15a8>0,
S16=$\frac{16}{2}$(a1+a16)=8(a8+a9)<0,
∴Sn>0的最大n是15,
∵等差数列{an}的前n项和为Sn,且满足a8>0,a8+a9<0,
∴该数列是递减数列,当n=8时,|a8|最小,且|S8|最大,
∴数列{$\frac{{S}_{n}}{{a}_{n}}$}(1≤n≤15)中最大的项为第8项
故答案为15,8.
点评 本题考查了等差数列的性质,考查了等差数列的前n项和,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.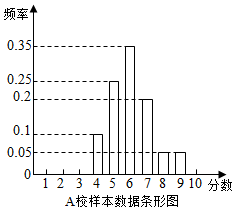 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
B校样本数据统计表
(Ⅰ)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:B校样本数据统计表
| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
13.若一组数据x1,x2…xn的方差为9,则数据2x1+1,2x2+1,…2xn+1的方差为( )
| A. | 9 | B. | 18 | C. | 19 | D. | 36 |
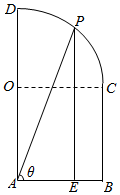 已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.
已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.