题目内容
4.设$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则(1)$\overrightarrow{a}$•$\overrightarrow{b}$=x1x2+y1y2;
(2)|$\overrightarrow{a}$|=$\sqrt{\overrightarrow{a}•\overrightarrow{a}}$=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$;
(3)$\overrightarrow{a}$⊥$\overrightarrow{b}$?$\overrightarrow{a}$•$\overrightarrow{b}$=0?x1x2+y1y2=0;
(4)cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{{x}_{1}{x}_{2}+{y}_{1}{y}_{2}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}}$.
分析 根据平面向量的运算性质计算.
解答 解:(1))$\overrightarrow{a}$•$\overrightarrow{b}$=x1x2+y1y2;
(2)|$\overrightarrow{a}$|=$\sqrt{\overrightarrow{a}•\overrightarrow{a}}$=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$;
(3)$\overrightarrow{a}$⊥$\overrightarrow{b}$?$\overrightarrow{a}•\overrightarrow{b}=0$?x1x2+y1y2=0;
(4)cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{{x}_{1}{x}_{2}+{y}_{1}{y}_{2}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}}$.
故答案为:(1)x1x2+y1y2;(2)$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$;(3)$\overrightarrow{a}•\overrightarrow{b}=0$,x1x2+y1y2=0;(4)$\frac{{x}_{1}{x}_{2}+{y}_{1}{y}_{2}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}}$.
点评 本题考查了平面向量的数量积运算的性质,属于基础题.

| A. | 若b∥a,则b∥α | B. | 若b⊥α,则b⊥a | C. | 若b∥α,则b∥a | D. | 若b⊥a,则b⊥α |
| A. | 1 | B. | 2 | C. | $\frac{12\sqrt{13}}{13}$ | D. | $\frac{28\sqrt{13}}{13}$ |
| A. | 知识结构图 | B. | 组织结构图 | C. | 工序流程图 | D. | 程序流程图 |
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
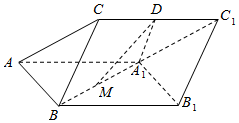 如图,三棱柱ABC-A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.