题目内容
已知函数f(x)=|2x+1|-|x|.
(1)求不等式f(x)>0的解集;
(2)若存在x∈R,使得f(x)≤m成立,求实数m的取值范围.
(1)求不等式f(x)>0的解集;
(2)若存在x∈R,使得f(x)≤m成立,求实数m的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)不等式即|2x+1|-|x|>0,分类讨论,把它转化为与之等价的3个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)由题意可得 m≥fmin(x),根据f(x)的解析式,求得fmin(x) 的值,可得m的范围.
(2)由题意可得 m≥fmin(x),根据f(x)的解析式,求得fmin(x) 的值,可得m的范围.
解答:
解:(1)不等式f(x)>0 即|2x+1|-|x|>0,
∴
①,或
②,或
③.
解①求得x<-1,解②求得-
<x<0,解③求得x≥0,
故原不等式的解集为{x|x<-1,或x>-
}.
(2)存在x∈R,使得f(x)≤m成立,故m≥fmin(x).
由于f(x)=
,
∴fmin(x)=f(-
)=-
,∴m≥-
,
即m的取值范围为[-
,+∞).
∴
|
|
|
解①求得x<-1,解②求得-
| 1 |
| 3 |
故原不等式的解集为{x|x<-1,或x>-
| 1 |
| 3 |
(2)存在x∈R,使得f(x)≤m成立,故m≥fmin(x).
由于f(x)=
|
∴fmin(x)=f(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即m的取值范围为[-
| 1 |
| 2 |
点评:本题主要考查绝对值不等式的解法,带有绝对值的函数,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF= 如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=
如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=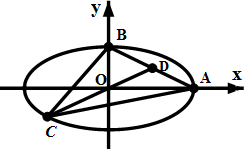 如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为
如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为