题目内容
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为[2,3],求实数a的值;
(2)若在(1)的条件下,存在实数t,使得f(
)≤m-f(-t)成立,求实数m的取值范围.
(1)若不等式f(x)≤6的解集为[2,3],求实数a的值;
(2)若在(1)的条件下,存在实数t,使得f(
| t |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)原不等式可化为|2x-a|≤6-a,解得a-3≤x≤3.再根据不等式f(x)≤6的解集为[2,3],可得a-3=2,从而求得a的值.
(2)由题意可得,|t-5|+|2t+5|+10≤m,根据函数y=|t-5|+|2t+5|+10=
,求得y的最小值,从而求得m的范围.
(2)由题意可得,|t-5|+|2t+5|+10≤m,根据函数y=|t-5|+|2t+5|+10=
|
解答:
解:(1)原不等式可化为|2x-a|≤6-a,
∴
,
解得a-3≤x≤3.
再根据不等式f(x)≤6的解集为[2,3],可得a-3=2,
∴a=5.
(2)∵f(x)=|2x-5|+5,f(
)≤m-f(-t),
∴|t-5|+5≤m-(|-2t-5|+5),
∴|t-5|+|2t+5|+10≤m,∵y=|t-5|+|2t+5|+10=
,
∴ymin=
,
∴m≥
,即m的范围是[
,+∞).
∴
|
解得a-3≤x≤3.
再根据不等式f(x)≤6的解集为[2,3],可得a-3=2,
∴a=5.
(2)∵f(x)=|2x-5|+5,f(
| t |
| 2 |
∴|t-5|+5≤m-(|-2t-5|+5),
∴|t-5|+|2t+5|+10≤m,∵y=|t-5|+|2t+5|+10=
|
∴ymin=
| 35 |
| 2 |
∴m≥
| 35 |
| 2 |
| 35 |
| 2 |
点评:本题主要考查绝对值不等式的解法,带有绝对值的函数,体现了转化的数学思想,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=
如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=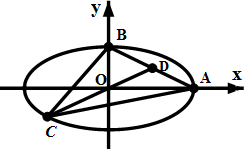 如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为
如图,已知中心在原点,焦点在x轴上的椭圆Γ的离心率为