题目内容
2.若($\sqrt{x}$+$\frac{a}{{x}^{2}}$)6的展开式中x-2的系数为15,则正实数a的值为1.分析 在二项展开式的通项公式中,令x的幂指数等于-1,求出r的值,再根据($\sqrt{x}$+$\frac{a}{{x}^{2}}$)6的展开式中x-2的系数为15,求得正实数a的值.
解答 解:($\sqrt{x}$+$\frac{a}{{x}^{2}}$)6的展开式的通项公式为Tr+1=C6r•ar•${x}^{3-\frac{5}{2}r}$,
令r=-2,可得3-$\frac{5}{2}$r=-2,∴r=2
∵($\sqrt{x}$+$\frac{a}{{x}^{2}}$)6的展开式中x-2的系数为15,
∴C62•a2=15,
∵a>0,
∴a=1,
故答案为:1.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
12.已知函数y=f(|x|)在[-1,1]上的图象如图甲所示,则y=f(x)在[-1,1]上的图象可能是图乙中的( )


| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
14.锐角△ABC中,a,b,c分别是角A,B,C的对边,若B=2A,则$\frac{b}{a}$的取值范围是( )
| A. | (0,2) | B. | ($\sqrt{2}$,2) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |
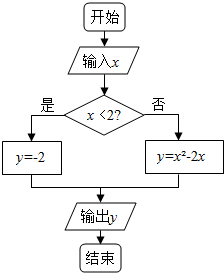 据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题
据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题