已知O是坐标原点.点A为平面区域x+y≥2x≤1y≤2上的一个动点.则|OA+OM|的最小值是．题目和参考答案——青夏教育精英家教网—

题目内容

已知O是坐标原点，点A（-1，0），若M（x，y）为平面区域

x+y≥2

x≤1

y≤2

上的一个动点，则|

|的最小值是

．

考点：简单线性规划

专题：数形结合

分析：由题意作出可行域，由向量的坐标加法运算求得

的坐标，把|

|转化为可行域内的点M（x，y）到定点N（1，0）的距离，数形结合可得答案．

解答： 解：由约束条件

x+y≥2

x≤1

y≤2

作平面区域如图，

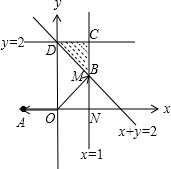
∵A（-1，0），M（x，y），
∴

=（-1，0）+（x，y）=（x-1，y），
则|

(x-1)2+y2

．
要使|

|最小，则可行域内的点M（x，y）到定点N（1，0）的距离最小．
由图可知，当M与B重合时满足题意．
联立

x=1

x+y=2

，得B（1，1）．
∴|

|的最小值是1．
故答案为：1．

点评：本题考查了简单的线性规划，考查了数形结合、转化与化归等解题思想方法，考查了向量模的求法，是中档题．

练习册系列答案

相关题目

），n=（sin2x，cos2x），定义函数f（x）=m•n．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）已知△ABC中，三边a，b，c所对的角分别为A，B，C，f（

）=0．
（i）若acosB+bcosA=csinC，求角B的大小；
（ii）记g（λ）=|

在△ABC中，角A，B，C所对的边分别为a，b，c，且2bcosA=2c+

a．
（Ⅰ）求角B；
（Ⅱ）求sinA+

sinC的取值范围．

设函数f（x）=cos（2x-

）-2sin²x．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若x∈[0，

]，求f（x）的最大值及相应的x值．

物体A以速度v=3t²+1在一直线上运动，在此直线上与物体A出发同时，物体B在物体A的正前方5m处以v=10t的速度运动，两物体相遇时，相遇地与物体A出发地的距离为

．

如图展示了一个由区间（0，1）到实数集R的映射过程：区间（0，1）中的实数m对应数轴上的点M（点A对应实数0，点B对应实数1），如图①；将线段AB围成一个圆，使两端点A、B恰好重合，如图②；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），在图形变化过程中，图①中线段AM的长度对应于图③中的弧ADM的长度，如图③，图③中直线AM与x轴交于点N（n，0），则m的象就是n，记作f（m）=n．

给出下列命题：①f（

）=1；②f（

）=0；③f（x）是奇函数；④f（x）在定义域上单调递增，则所有真命题的序号是

．（填出所有真命题的序号）

二项式（x-

）⁶（a＞0）展开式中x²项的系数为15，则实数a=

．

如图是一程序框图，则其输出结果为26，则判断框内为

．

已知i是虚数单位，则复数z=i³•（-1+2i）的虚部为（　　）

试题分类