题目内容
已知函数f（x）=ax3+bx-2，若f（2014）=10，则f（-2014）的值为 ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：先将f（2014）表示出来，注意必要化简，然后将f（-2014）表示出来，联系与f（2014）的关系，整体代入即可．
解答：
解：由已知得f（2014）=a×20143+b×2014-2=10，
所以a×20143+b×2014=12．
则f（-2014）=a×（-2014）3-b×（-2014）-2
=-（a×20143+b×2014）-2=-14．
故答案为-14．
所以a×20143+b×2014=12．
则f（-2014）=a×（-2014）3-b×（-2014）-2
=-（a×20143+b×2014）-2=-14．
故答案为-14．
点评：本题考查了利用函数的奇偶性求函数值的方法，注意整体代换思想．
练习册系列答案
相关题目
已知向量
=（m，2），向量
=（2，-3），若|
+
|=|
-
|，则实数m的值是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、3 | ||
C、
| ||
| D、-3 |
一几何体的三视图如图所示，若主视图和左视图都是等腰直角三角形，直角边长为1，则该几何体外接球的表面积为（ ）| A、4π | B、3π | C、2π | D、π |
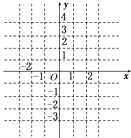已知函数f（x）是定义域为R的奇函数，当x＞0时，f（x）=x2-2x，