题目内容
设数列{an}为等差数列,且a5=14,a7=20,数列{bn}的前n项和为Sn,b1=
且3Sn=Sn-1+2(n≥2,n∈N).
(1)求数列{an},{bn}的通项公式;
(2)若cn=an•bn,n=1,2,3,…,求数列{cn}的前n项和Tn.
| 2 |
| 3 |
(1)求数列{an},{bn}的通项公式;
(2)若cn=an•bn,n=1,2,3,…,求数列{cn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用等差数列的性质,求出首项和公差,由此能求出an=3n-1.由3Sn=Sn-1+2(n≥2,n∈N),得3Sn=Sn-bn+2,即bn=2-2Sn,由此能求出bn=2•
.
(Ⅱ)由cn=an•bn=2(3n-1)•
,利用错位相减法能求出数列{cn}的前n项和Tn.
| 1 |
| 3n |
(Ⅱ)由cn=an•bn=2(3n-1)•
| 1 |
| 3n |
解答:
解:(Ⅰ)∵数列{an}为等差数列,且a5=14,a7=20,公差d=
(a7-a5)=3,
∴a1+4×3=14,解得a1=2,
∴an=2+(n-1)×3=3n-1.
由3Sn=Sn-1+2(n≥2,n∈N),得3Sn=Sn-bn+2,即bn=2-2Sn,
∴b2=2-(b1+b2),又b1=
,∴b2=
,
=
=
,
由3Sn=Sn-1+2,当n≥3时,得3Sn-1=Sn-2+2,
两式相减得:3(Sn-Sn-1)=Sn-1-Sn-2,即3bn=bn-1,
∴
=
(n≥3)
又
=
,∴{bn}是以b1=
为首项,
为公比的等比数列,于是bn=2•
.
(Ⅱ)cn=an•bn=2(3n-1)•
,
∴Tn=2[2×
+5×
+8×
+…+(3n-1)×
],
Tn=2[2×
+5×
+…+(3n-4)×
+(3n-1)×
],
两式相减得
Tn=2[3×
+3×
+3×
+…+3×
-
-(3n-1)×
]
=2[1+
+
+
+…+
-
-(3n-1)×
]
=2×
-2×
-(3n-1)×
=
-
-
,
∴Tn=
-
.
| 1 |
| 2 |
∴a1+4×3=14,解得a1=2,
∴an=2+(n-1)×3=3n-1.
由3Sn=Sn-1+2(n≥2,n∈N),得3Sn=Sn-bn+2,即bn=2-2Sn,
∴b2=2-(b1+b2),又b1=
| 2 |
| 3 |
| 2 |
| 9 |
| b2 |
| b1 |
| ||
|
| 1 |
| 3 |
由3Sn=Sn-1+2,当n≥3时,得3Sn-1=Sn-2+2,
两式相减得:3(Sn-Sn-1)=Sn-1-Sn-2,即3bn=bn-1,
∴
| bn |
| bn-1 |
| 1 |
| 3 |
又
| b2 |
| b1 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3n |
(Ⅱ)cn=an•bn=2(3n-1)•
| 1 |
| 3n |
∴Tn=2[2×
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
两式相减得
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 3n+1 |
=2[1+
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n-1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
=2×
1-
| ||
1-
|
| 1 |
| 3 |
| 1 |
| 3n+1 |
=
| 7 |
| 3 |
| 3 |
| 3n |
| 3n-1 |
| 3n+1 |
∴Tn=
| 7 |
| 2 |
| n+9 |
| 3n |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
若双曲线的标准方程为
-
=1,则它的渐近线方程为( )
| x2 |
| 8 |
| y2 |
| 4 |
A、x±
| ||
B、
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
从2011名学生中选取50名组成参观团,若采用下面的方法选取,先用简单随机抽样法从2011人中剔除11人,剩下的2000人再按系统抽样的方法进行,则每人入选的概率( )
| A、不全相等 | ||
| B、均不相等 | ||
C、都相等且为
| ||
D、都相等且为
|
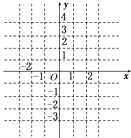 已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x,
已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x,