题目内容
已知函数f(x)=
，则f(f(
))=（ ）
|
| π |
| 4 |
| A、2 | B、1 | C、-2 | D、-1 |
考点：函数的值
专题：函数的性质及应用
分析：根据分段函数的表达式，直接代入即可得到结论．
解答：
解：由分段函数可知f（
）=-tan
=-1，
f（-1）=-2，
∴f（f（
））=f（-1）=-2，
故选：C．
| π |
| 4 |
| π |
| 4 |
f（-1）=-2，
∴f（f（
| π |
| 4 |
故选：C．
点评：本题主要考查函数值的计算，利用分段函数直接代入即可，注意变量的取值范围．
练习册系列答案
相关题目
动点P（m，n）到直线l：x=-5的距离为λ
，点P的轨迹为双曲线（且原点O为准线l对应的焦点），则λ的取值为（ ）
| m2+n2 |
| A、λ∈R | B、λ=1 |
| C、λ＞1 | D、0＜λ＜1 |
给出下列命题，其中正确的有（ ）
①存在实数x，使得sinx+cosx=
；
②若cosα＞0，则α是第一象限角或第四象限角；
③函数y=sin(
x+
)是偶函数；
④若α是第二象限角，且P（x，y）是α终边上异于坐标原点的一点，则cosα=
．
①存在实数x，使得sinx+cosx=
| 3 |
| 2 |
②若cosα＞0，则α是第一象限角或第四象限角；
③函数y=sin(
| 3 |
| 4 |
| π |
| 2 |
④若α是第二象限角，且P（x，y）是α终边上异于坐标原点的一点，则cosα=
| -x | ||
|
| A、1个 | B、2个 | C、3个 | D、4个 |
公务员考试分笔试和面试，笔试的通过率为20%，最后的录取率为4%，已知某人已经通过笔试，则他最后被录取的概率为（ ）
| A、20% | B、24% |
| C、16% | D、4% |
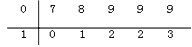如图所示的茎叶图记录了一组数据，关于这组数据给出了如下四个结论：①众数是9；②平均数10；③中位数是9或10；④方差是3.4，其中正确命题的个数是（ ）