题目内容
4.等比数列{an}中,a3=-1,求a1a2a3a4a5的值.分析 利用等比数列的性质即可得出.
解答 解:由等比数列的性质可得:a1a2a3a4a5=(a1a5)(a2a4)•a3=${a}_{3}^{2}•{a}_{3}^{2}$•a3=(-1)5=-1.
点评 本题考查了等比数列的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知二次函数f(x)=2x2-(a-2)x-2a2-a,若在区间[0,1]内至少存在一个实数b,使f(b)>0,则实数a的取值范围是( )
| A. | (-2,1) | B. | $(-\frac{1}{2},\;2)$ | C. | $(-2,\;-\frac{1}{2})$ | D. | $(-\frac{1}{2},\;1)$ |
19.已知数列{an}满足an=tan$\frac{nπ}{3}$,那么a1+a2+…+a2016的值为( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 0 |
9.在如表数表中,已知每行、每列中的数都成等差数列,那么,位于表中的第n行、第(n+1)列的数是( )
| 第1列 | 第2列 | 第3列 | … | |
| 第1行 | 1 | 2 | 3 | … |
| 第2行 | 2 | 4 | 6 | … |
| 第3行 | 3 | 6 | 9 | … |
| … | … | … | … | … |
| A. | n2-n+1 | B. | n2-n | C. | n2+n | D. | n2+n+2 |
13.已知等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为( )
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
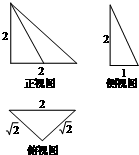 如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.
如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.