题目内容
14．已知二次函数f（x）=2x2-（a-2）x-2a2-a，若在区间[0，1]内至少存在一个实数b，使f（b）＞0，则实数a的取值范围是（ ）| A． | （-2，1） | B． | $（-\frac{1}{2}，\;2）$ | C． | $（-2，\;-\frac{1}{2}）$ | D． | $（-\frac{1}{2}，\;1）$ |
分析 由题意可得：f（0）＞0，或f（1）＞0，解出即可得出．
解答 解：由题意可得：f（0）＞0，或f（1）＞0，
即-2a2-a＞0，或2-（a-2）-2a2-a＞0，
解得$-\frac{1}{2}＜a＜$0，或-2＜a＜1．
∴实数a的取值范围是（-2，1）．
故选：A．
点评 本题考查了二次函数的性质、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
3．函数$f（x）={x^{\frac{1}{2}}}-2+{log_2}x$的零点所在区间是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，+∞） |
2．函数y=（$\frac{1}{2}$）${\;}^{{x}^{2}}$+4x的值域为（ ）
| A． | [0，16] | B． | （0，16] | C． | （16，+∞） | D． | [16，+∞） |
9．已知函数f（x）=-3sin2x-4cosx+2，则该函数的最大值和最小值的差为（ ）
| A． | 6 | B． | 4 | C． | $\frac{25}{3}$ | D． | -$\frac{7}{3}$ |
19．函数f（x）的导函数为f'（x），且满足f（x）=3x2+2xf'（2），则f'（5）的值为（ ）
| A． | 5 | B． | 1 | C． | 6 | D． | -2 |
6．已知函数f（x）=x+$\frac{a}{x}$在区间[1，+∞）上递增，则实数a的取值范围为（ ）
| A． | （0，+∞） | B． | （-∞，0） | C． | （0，1] | D． | （-∞，1] |
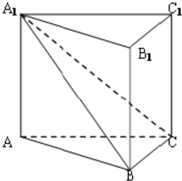如图，在直三棱柱ABC-A1B1C1中，平面A1BC丄侧面A1AB B1，且 AA1=AB=2．