题目内容
12.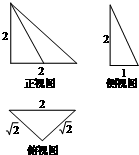 如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.
如图是一个空间几何体的三视图,该几何体的外接球的体积记为V1,俯视图绕底边所在直线旋转一周形成的几何体的体积记为V2,则V1:V2=4$\sqrt{2}$.
分析 判断三视图复原的几何体的形状,底面为等腰直角三角形,一条侧棱垂直底面的一个顶点,结合数据求出外接球的半径,由此能求出结果.
解答 解:三视图复原的几何体如图,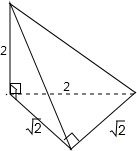
它是底面为等腰直角三角形,一条侧棱垂直底面的一个顶点,
它的外接球,就是扩展为长方体的外接球,
外接球的直径是2$\sqrt{2}$,
该几何体的外接球的体积V1=$\frac{4}{3}$π($\sqrt{2}$)3=$\frac{8\sqrt{2}}{3}$π.
V2=2×($\frac{1}{3}×π×{1}^{2}×1$)=$\frac{2}{3}$π,
∴V1:V2=$\frac{8\sqrt{2}}{3}$π:$\frac{2}{3}$π=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查三视图求几何体的外接球的体积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
相关题目
2.函数y=($\frac{1}{2}$)${\;}^{{x}^{2}}$+4x的值域为( )
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |
20.(1+tan18°)(1+tan27°)的值是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
7.已知A={-1,2},B={x|mx+1=0},若A∪B=A,则实数m的取值所成的集合是( )
| A. | $\left\{{-1,\frac{1}{2}}\right\}$ | B. | $\left\{{-\frac{1}{2},1}\right\}$ | C. | $\left\{{-1,0,\frac{1}{2}}\right\}$ | D. | $\left\{{-\frac{1}{2},0,1}\right\}$ |
1.已知函数是定义在R上的奇函数,当x>0时,f(x)=-x2-x,则f(-2)=( )
| A. | 6 | B. | -6 | C. | 2 | D. | -2 |
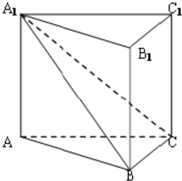 如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB B1,且 AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB B1,且 AA1=AB=2.