题目内容

15．三个实数成等差数列，首项是9，若将第二项加2、第三项加20可使得这三个数依次构成等比数列{an}，则a3的所有取值中的最小值是（　　）
A．1B．4C．36D．49

分析 设首项为9的等差数列分别为9，9+d，9+2d，则（11+d）2=9（29+2d），由此能求出a3的所有可能取值中最小值．

解答 解：设首项为9的等差数列分别为9，9+d，9+2d，
其中d为公差，又9，11+d，29+2d成等比数列，
则（11+d）2=9（29+2d），解得d=-14或d=10，
当d=-14时，数列{an}的三项依次为9，-3，1；
当d=10时，数列{an}的三项依次为9，21，49．
故a3的所有可能取值中最小的是1，
故选：A．

点评 本题考查数列中第三项的最小值的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

练习册系列答案
相关题目
5．有6名同学参加甲、乙、丙3项课外活动，每位同学必须参加一项活动不能同时参加两项，且每项活动都要有人参加，其中甲活动最多安排2人，则不同的安排方法有（　　）种．
A．320B．360C．384D．390
6．设α∈（$\frac{π}{2}$，π），且tanα=-2，则sinα=$\frac{2\sqrt{5}}{5}$，cosα=$-\frac{\sqrt{5}}{5}$．
3．直线x-3y+2=0不经过（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
10．在△ABC中，AB=5，AC=7，BC=8，则$\overrightarrow{AB}$•$\overrightarrow{BC}$=-20．
20．在△ABC中，若（a+b+c）（b+c-a）=bc，且sinA=2sinBcosC，试判断△ABC的形状．
7．某城市居民月生活用水收费标准为$W（t）=\left\{{\begin{array}{l}{1.6t，（{0≤t＜2}）}\\{2.7t，（{2≤t＜3.5}）}\\{4.0t，（{3.5≤t≤4.5}）}\end{array}}\right.$（t为用水量，单位：吨；W为水费，单位：元），从该市抽取100户居民的月均用水量的频率分布直方图如图所示． 

（Ⅰ）求这100户居民月均用水量的中位数及平均水费；
（Ⅱ）连续10个月，每月从这100户中随机抽取一户，若抽到的用户当月所交水费少于9.45元，则对其予以奖励．设X为获奖户数，求X的数学期望．
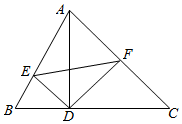4．在△ABC中，AB=4，AC=6，∠BAC=60°．点A在边BC上的投影为点D．
（1）试求线段AD的长度；
（2）设点D在边AB上的投影为点E，在边AC上的投影为F，试求线段EF的长度．
5．已知f（x）=Asin（2x+φ），其中A＞0．
（1）若?x∈R，使f（x+a）-f（x）=2A成立，则实数a的最小值是$\frac{π}{2}$；
（2）若A=1，则f（x+$\frac{π}{6}$）-f（x）的最大值为1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网