题目内容
6.设α∈($\frac{π}{2}$,π),且tanα=-2,则sinα=$\frac{2\sqrt{5}}{5}$,cosα=$-\frac{\sqrt{5}}{5}$.分析 由同角三角函数基本关系解方程组可得sinα和cosα,结合角的范围可得.
解答 解:∵tanα=-2,∴sinα=-2cosα,
联立sin2α+cos2α=1可解得$\left\{\begin{array}{l}{sinα=-\frac{2\sqrt{5}}{5}}\\{cosα=\frac{\sqrt{5}}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{sinα=\frac{2\sqrt{5}}{5}}\\{cosα=-\frac{\sqrt{5}}{5}}\end{array}\right.$,
∵α∈($\frac{π}{2}$,π),∴cosα<0,
故$\left\{\begin{array}{l}{sinα=\frac{2\sqrt{5}}{5}}\\{cosα=-\frac{\sqrt{5}}{5}}\end{array}\right.$符合题意.
故答案为:$\frac{2\sqrt{5}}{5}$;$-\frac{\sqrt{5}}{5}$.
点评 本题考查同角三角函数基本关系,涉及方程组的解法,属基础题.

练习册系列答案
相关题目
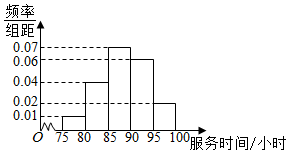 某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.