题目内容
5.已知f(x)=Asin(2x+φ),其中A>0.(1)若?x∈R,使f(x+a)-f(x)=2A成立,则实数a的最小值是$\frac{π}{2}$;
(2)若A=1,则f(x+$\frac{π}{6}$)-f(x)的最大值为1.
分析 (1)根据正弦函数的图象和性质可得f(x+a)=A,f(x)=-A,故a的最小值为f(x)的半周期.
(2)使用和角公式化简,利用三角函数的性质得出最大值.
解答 解:(1)∵f(x)的最大值为A,最小值为-A,f(x+a)-f(x)=2A,
∴f(x+a)=A,f(x)=-A,∴a的最小值为f(x)的半周期.
∵f(x)的周期T=π,∴a的最小值为$\frac{π}{2}$.
(2)f(x+$\frac{π}{6}$)=sin(2x+$\frac{π}{3}$+φ),f(x)=sin(2x+φ).
∴f(x+$\frac{π}{6}$)-f(x)=sin(2x+$\frac{π}{3}$+φ)-sin(2x+φ)=$\frac{1}{2}$sin(2x+φ)+$\frac{\sqrt{3}}{2}$cos(2x+φ)-sin(2x+φ)
=$\frac{\sqrt{3}}{2}$cos(2x+φ)-$\frac{1}{2}$sin(2x+φ)
=cos(2x+$\frac{π}{6}$+φ).
∴f(x+$\frac{π}{6}$)-f(x)的最大值为1.
故答案为$\frac{π}{2}$,1.
点评 本题考查了正弦函数的图象与性质,三角函数的恒等变换,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.阅读算法框图,如果输出的函数值在区间[1,8]上,则输入的实数x的取值范围是( )
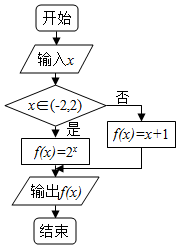

| A. | [0,2) | B. | [2,7] | C. | [2,4] | D. | [0,7] |
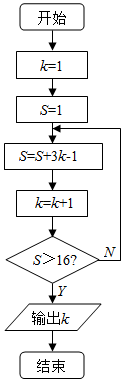
20.如图是一个程序框图,则输出S的值是( )


| A. | 84 | B. | 35 | C. | 26 | D. | 10 |
17.执行如图所示的程序框图,则输出的s=( )
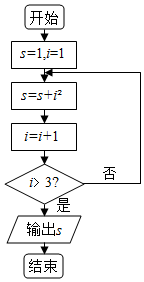

| A. | 6 | B. | 15 | C. | 25 | D. | 3 |
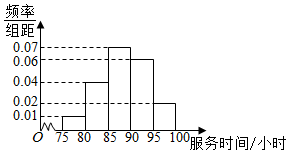 某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.