题目内容
1.函数y=log2(x-x2)的定义域为( )| A. | (0,1) | B. | (-1,0) | C. | (1,+∞) | D. | (-∞,0) |
分析 根据对数函数的性质求出函数的定义域即可.
解答 解:由题意得:
x-x2>0,
解得:0<x<1,
故选:A.
点评 本题考查了求函数的定义域问题,考查对数函数的性质,是一道基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
9.下列各数中最小的数是( )
| A. | 111111(2) | B. | 1000(4) | C. | 210(6) | D. | 85(9) |
13.对于二次函数y=-$\frac{1}{4}$x2+x-4,下列说法正确的是( )
| A. | 当x>0时,y随x的增大而增大 | B. | 当x=2时,y有最大值-3 | ||
| C. | 图象的顶点坐标为(-2,-7) | D. | 图象与x轴有两个交点 |
10.某树苗培育基地为了解其基地内榕树树苗的长势情况,随机抽取了100株树苗,分别测出它们的高度(单位:cm),并将所得数据分组,画出频率分布表如表:
(1)求如表中a、b的值;
(2)估计该基地榕树树苗平均高度;
(3)若将这100株榕树苗高度分布的频率视为概率,从培育基地的榕树苗中随机选出4株,其中在[104,106)内的有X株,求X的分布列和期望.
| 组 距 | 频 数 | 频 率 |
| [100,102) | 16 | 0.16 |
| [102,104) | 18 | 0.18 |
| [104,106) | 25 | 0.25 |
| [106,108) | a | b |
| [108,110) | 6 | 0.06 |
| [110,112) | 3 | 0.03 |
| 合计 | 100 | 1 |
(2)估计该基地榕树树苗平均高度;
(3)若将这100株榕树苗高度分布的频率视为概率,从培育基地的榕树苗中随机选出4株,其中在[104,106)内的有X株,求X的分布列和期望.
11.设全集∪={a,b,c,d},集合M={ a,c,d },N={b,d},则(∁UM)∩N等于( )
| A. | {b} | B. | {d} | C. | {a,c} | D. | {b,d} |
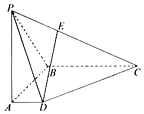 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.