题目内容
直线x-y+2=0与圆x2+y2=4相交于A,B,则弦长|AB|= .
考点:直线与圆相交的性质
专题:直线与圆
分析:易得圆的圆心和半径,由距离公式可得圆心到直线的距离d,由勾股定理可得|AB|=2
,代值计算可得.
| r2-d2 |
解答:
解:∵圆x2+y2=4的圆心为(0,0),半径r=2,
∴圆心到直线x-y+2=0的距离d=
=
,
∴弦长|AB|=2
=2
故答案为:2
∴圆心到直线x-y+2=0的距离d=
| |0-0+2| | ||
|
| 2 |
∴弦长|AB|=2
| r2-d2 |
| 2 |
故答案为:2
| 2 |
点评:本题考查直线与圆的位置关系,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是( )
| A、直线与圆相交且过圆心 |
| B、直线与圆相交但不过圆心 |
| C、相切 |
| D、相离 |
已知集合P={x|-1≤x≤1},M={a},若P∪M=P,则a的取值范围是( )
| A、(-∞,-1] |
| B、[1,+∞) |
| C、[-1,1] |
| D、(-∞,-1]∪[1,+∞) |
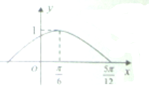 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-