题目内容
已知直线l的极坐标方程为ρ(sinθ+cosθ)=1,曲线C的参数方程为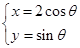 (θ为参数).
(θ为参数).
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)设直线l与曲线C交于A,B四两点,原点为O,求△ABO的面积.
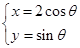 (θ为参数).
(θ为参数).(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)设直线l与曲线C交于A,B四两点,原点为O,求△ABO的面积.
(1)x+y-1=0;(2) .
.
 .
.本试题主要考查极坐标系和参数方程的综合运用。直线与椭圆的位置关系的问题。
解:(Ⅰ)直线的直角坐标方程为:x+y-1=0;(3分)
(Ⅱ)原点到直线的距离 d= ,
,
直线参数方程为: (t为参数)曲线C的直角坐标方程为:
(t为参数)曲线C的直角坐标方程为: 
联立得: 5t2+2 2t-6=0,求得 AB=|t1-t2|=
2t-6=0,求得 AB=|t1-t2|=
所以 S△ABO=12AB•d= (10分)
(10分)
解:(Ⅰ)直线的直角坐标方程为:x+y-1=0;(3分)
(Ⅱ)原点到直线的距离 d=
 ,
,直线参数方程为:
 (t为参数)曲线C的直角坐标方程为:
(t为参数)曲线C的直角坐标方程为: 
联立得: 5t2+2
 2t-6=0,求得 AB=|t1-t2|=
2t-6=0,求得 AB=|t1-t2|=
所以 S△ABO=12AB•d=
 (10分)
(10分)
练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 中,已知曲线
中,已知曲线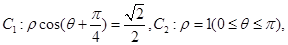
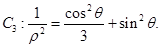 设
设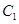 与
与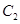 交于点
交于点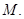
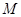 的极坐标;
的极坐标;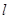 过点
过点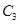 交于两个不同的点
交于两个不同的点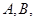 求
求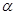
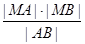 的最小值.
的最小值.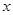 轴的正半轴为极轴建极坐标系,两种坐标系取相同的单位长度. 已知曲线
轴的正半轴为极轴建极坐标系,两种坐标系取相同的单位长度. 已知曲线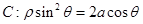
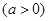 ,过点
,过点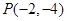 的直线
的直线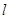 的参数方程为
的参数方程为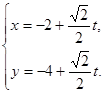 直线
直线 分别交于
分别交于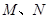 .若
.若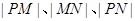 成等比数列,则实数
成等比数列,则实数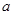 的值为 .
的值为 .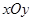 中,以原点为极点,
中,以原点为极点,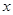 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线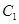 :
: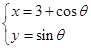 (
(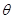 为参数)和曲线
为参数)和曲线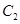 :
: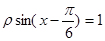 上,则
上,则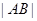 的最小值为 .
的最小值为 .  ,直线
,直线 的过点A且与极轴所成的角为
的过点A且与极轴所成的角为 ,则直线
,则直线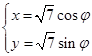 (
(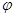 为参数,
为参数,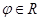 )上的点到曲线
)上的点到曲线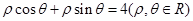 的最短距离是
的最短距离是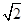 -
-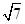
 的圆心的极坐标是( )
的圆心的极坐标是( )


