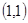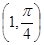题目内容
在极坐标系 中,已知曲线
中,已知曲线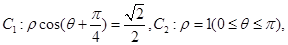
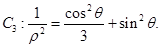 设
设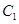 与
与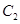 交于点
交于点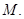
(I)求点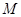 的极坐标;
的极坐标;
(II)若动直线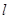 过点
过点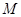 ,且与曲线
,且与曲线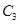 交于两个不同的点
交于两个不同的点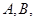 求
求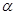
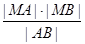 的最小值.
的最小值.
 中,已知曲线
中,已知曲线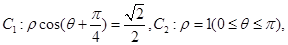
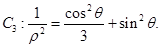 设
设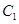 与
与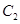 交于点
交于点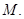
(I)求点
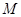 的极坐标;
的极坐标;(II)若动直线
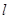 过点
过点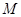 ,且与曲线
,且与曲线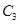 交于两个不同的点
交于两个不同的点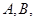 求
求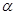
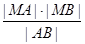 的最小值.
的最小值.(I)点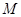 的极坐标为
的极坐标为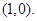
(II)当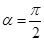 时,
时,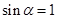 ,
,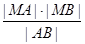 有最小值
有最小值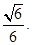
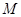 的极坐标为
的极坐标为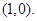
(II)当
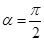 时,
时,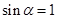 ,
,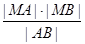 有最小值
有最小值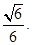
(I)先求出曲线C1和曲线C2的普通方程,然后联立解方程组即可得到点M的直角坐标,再化成极坐标.
(II)设直线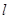 的参数方程为
的参数方程为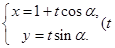 为参数),代入曲线
为参数),代入曲线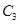 的直角坐标方程并整理得
的直角坐标方程并整理得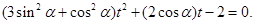
然后根据参数t的几何意义可知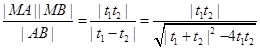 再借助韦达定理转化为关于
再借助韦达定理转化为关于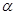 的三角函数来求最值.
的三角函数来求最值.
解:(I)由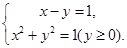 解得点
解得点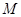 的直角坐标为
的直角坐标为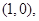 因此点
因此点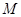 的极坐标为
的极坐标为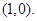
(II)设直线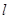 的参数方程为
的参数方程为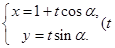 为参数),代入曲线
为参数),代入曲线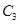 的直角坐标方程并整理得
的直角坐标方程并整理得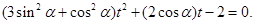
设点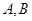 对应的参数分别为
对应的参数分别为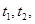 则
则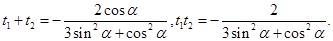
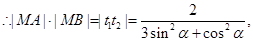
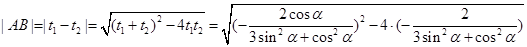
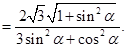
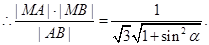
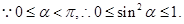
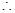 当
当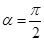 时,
时,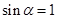 ,
,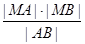 有最小值
有最小值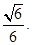
(II)设直线
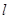 的参数方程为
的参数方程为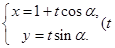 为参数),代入曲线
为参数),代入曲线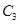 的直角坐标方程并整理得
的直角坐标方程并整理得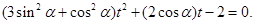
然后根据参数t的几何意义可知
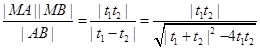 再借助韦达定理转化为关于
再借助韦达定理转化为关于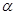 的三角函数来求最值.
的三角函数来求最值.解:(I)由
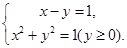 解得点
解得点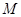 的直角坐标为
的直角坐标为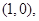 因此点
因此点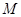 的极坐标为
的极坐标为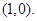
(II)设直线
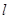 的参数方程为
的参数方程为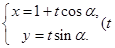 为参数),代入曲线
为参数),代入曲线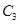 的直角坐标方程并整理得
的直角坐标方程并整理得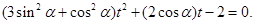
设点
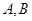 对应的参数分别为
对应的参数分别为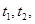 则
则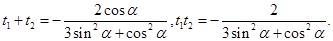
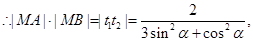
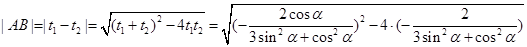
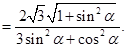
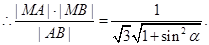
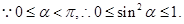
 当
当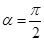 时,
时,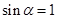 ,
,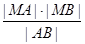 有最小值
有最小值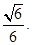

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
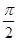 ).若直线l过点P,且倾斜角为
).若直线l过点P,且倾斜角为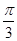 ,圆C以M为圆心, 4为半径.
,圆C以M为圆心, 4为半径.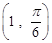 为圆心,1为半径的圆的极坐标方程是 .
为圆心,1为半径的圆的极坐标方程是 .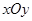 中,直线
中,直线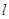 的参数方程为
的参数方程为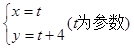 .曲线
.曲线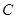 的参数方程为
的参数方程为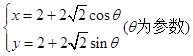 ,则直线
,则直线 个
个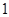 个
个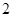 个
个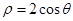 的圆心到直线
的圆心到直线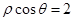 的距离是_____________.
的距离是_____________. 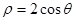 关于直线
关于直线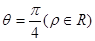 对称的圆的的极坐标方程是 .
对称的圆的的极坐标方程是 .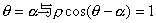 的位置关系是( )
的位置关系是( )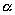 有关,不确定
有关,不确定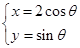 (θ为参数).
(θ为参数).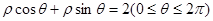 与
与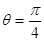 的交点的极坐标是( )
的交点的极坐标是( )