题目内容
函数y=
的定义域、值域及图象的对称中心分别为 ．
| x+2 |
| x-6 |
考点：函数的定义域及其求法,函数的值域
专题：函数的性质及应用
分析：根据分式函数的性质即可得到结论．
解答：
解：y=
=
=1+
，
则函数的定义域为{x|x≠6}，
∵
≠0，
∴1+
≠1，
即函数的值域为{y|y≠1}，
则函数的对称中心为（6，1）．
故答案为：{x|x≠6}，{y|y≠1}，（6，1）
| x+2 |
| x-6 |
| x-6+8 |
| x-6 |
| 8 |
| x-6 |
则函数的定义域为{x|x≠6}，
∵
| 8 |
| x-6 |
∴1+
| 8 |
| x-6 |
即函数的值域为{y|y≠1}，
则函数的对称中心为（6，1）．
故答案为：{x|x≠6}，{y|y≠1}，（6，1）
点评：本题主要考查分式函数的性质，利用分子常数化是解决本题的关键．
练习册系列答案
相关题目
已知平面上两点M（-5，0）和N（5，0），若直线上存在点P使|PM|-|PN|=6，则称该直线为“单曲型直线”，下列直线中是“单曲型直线”的是（ ）
①y=x+1； ②y=2； ③y=
x； ④y=2x+1．
①y=x+1； ②y=2； ③y=
| 4 |
| 3 |
| A、①③ | B、①② | C、②③ | D、③④ |
已知点M（x，y）为平面区域
内的一个动点，则
的最小值为（ ）
|
| (x+1)2+y2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
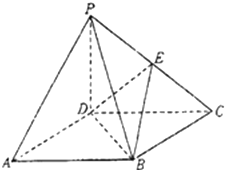如图，四棱锥P-ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．