题目内容
13.随着网络的发展,人们可以在网路上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐,为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户按年龄分组进行访谈,统计结果如下表:| 组号 | 年龄 | 访谈人数 | 愿意使用 |
| 1 | [20,30) | 5 | 5 |
| 2 | [30,40) | 10 | 10 |
| 3 | [40,50) | 15 | 12 |
| 4 | [50,60) | 14 | 8 |
| 5 | [60,70) | 6 | 2 |
(2)若从第5组的被调查访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(3)按以上统计数据填写下面2×2列联表,并判断以50岁为分界点,能否在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关;
| 年龄不低于50岁的人数 | 年龄低于50岁的人数 | 合计 | |
| 愿意使用的人数 | |||
| 不愿意使用的人数 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)第2、3、4组的比例为10:12:8=5:6:4,即可得出结论;
(2)利用对立事件求出相应的概率;
(3)由列联表数据代入公式求出K2,从而得到在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.
解答 解:(1)第2、3、4组的比例为10:12:8=5:6:4,
∴用分层抽样的方法抽取15人,则各组应分别抽取5,6,4人;
(2)若从第5组的被调查访谈人中随机选取2人进行追踪调查,有C62=15种方法,则2人中至少有1人愿意选择此款“流量包”套餐的概率为1-$\frac{{C}_{4}^{2}}{15}$=$\frac{3}{5}$.
(3)2×2列联表
| 年龄不低于50岁的人数 | 年龄低于50岁的人数 | 合计 | |
| 愿意使用的人数 | 10 | 27 | 37 |
| 不愿意使用的人数 | 10 | 3 | 13 |
| 合计 | 20 | 30 | 50 |
∴在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查独立性检验知识的运用,是中档题.

练习册系列答案
相关题目
3.函数f(x)=2|sinx|的最小正周期为( )
| A. | 2π | B. | $\frac{3π}{2}$ | C. | π | D. | $\frac{π}{2}$ |
1.已知z=$\frac{1-3i}{3+i}$(i为虚数单位),则z的共轭复数的虚部为( )
| A. | -i | B. | i | C. | -1 | D. | 1 |
8.已知函数f(x)=(ex-e-x)x,f(log5x)+f(log${\;}_{\frac{1}{5}}$x)≤2f(1),则x的取值范围是( )
| A. | [$\frac{1}{5}$,1] | B. | [1,5] | C. | [$\frac{1}{5}$,5] | D. | (-∞,$\frac{1}{5}$]∪[5,+∞) |
2.若集合A={x|x2-x-6>0},集合B={x|-1<x<4},则A∩B等于( )
| A. | ∅ | B. | (-2,3) | C. | (2,4) | D. | (3,4) |
3.已知直线a,b,平面α,β,a?α,b?α,则a∥β,b∥β是α∥β的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
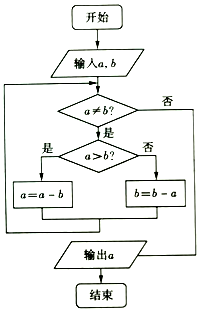 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )
如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )