题目内容
用数学归纳法证明12+32+52+…+(2n-1)2=
n(4n2-1)过程中,由n=k递推到n=k+1时,不等式左边增加的项为( )
| 1 |
| 3 |
| A、(2k)2 |
| B、(2k+3)2 |
| C、(2k+2)2 |
| D、(2k+1)2 |
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:可从证题的第二步起,假设n=k时等式成立(写出等式),去证明n=k+1时,等式成立(写出等式),观察即可.
解答:
解:用数学归纳法证明12+32+52+…+(2n-1)2=
n(4n2-1)的过程中,
第二步,假设n=k时等式成立,即12+32+52+…+(2k-1)2=
k(4k2-1),
那么,当n=k+1时,12+32+52+…+(2k-1)2+(2k+1)2=
k(4k2-1)+(2k+1)2,
等式左边增加的项是(2k+1)2,
故选:D.
| 1 |
| 3 |
第二步,假设n=k时等式成立,即12+32+52+…+(2k-1)2=
| 1 |
| 3 |
那么,当n=k+1时,12+32+52+…+(2k-1)2+(2k+1)2=
| 1 |
| 3 |
等式左边增加的项是(2k+1)2,
故选:D.
点评:本题考查数学归纳法,掌握用数学归纳法的证题步骤与思路是关键,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
若直线mx+ny+2=0(m>0,n>0)截得圆(x+3)2+(y+1)2=1的弦长为2,则
+
的最小值为( )
| 1 |
| m |
| 3 |
| n |
| A、6 | B、8 | C、10 | D、12 |
对于函数f(x)=sin(πx+
),下列命题正确的是( )
| π |
| 2 |
| A、f(x)的周期为π,且在[0,1]上单调递增 |
| B、f(x)的周期为2,且在[0,1]上单调递减 |
| C、f(x)的周期为π,且在[-1,0]上单调递增 |
| D、f(x)的周期为2,且在[-1,0]上单调递减 |
Sn是数列{an}的前n项和,an=
,则S1=1-
,S2=1-
,S3=1-
,S4=1-
,由此可以归纳出( )
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、Sn=1-
| ||
B、Sn=1-
| ||
C、Sn=1-
| ||
D、Sn=1-
|
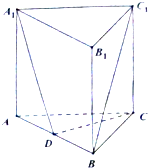 如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.
如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.