题目内容
13.将函数y=$\sqrt{2}$cos2x的图象向右平移$\frac{π}{24}$个单位后,与函数f(x)=cos(2x-$\frac{π}{3}$)+cos(2x+$\frac{π}{6}$)的图象重合.分析 由条件利用三角恒等变换化简函数f(x)的解析式,再根据y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:根据函数f(x)=cos(2x-$\frac{π}{3}$)+cos(2x+$\frac{π}{6}$)=2cos(2x-$\frac{π}{12}$)cos(-$\frac{π}{4}$)
=$\sqrt{2}$cos(2x-$\frac{π}{12}$)=$\sqrt{2}$cos2(x-$\frac{π}{24}$),
故把函数y=$\sqrt{2}$cos2x的图象向右平移$\frac{π}{24}$个单位,可得f(x)的图象,
故答案为:右;$\frac{π}{24}$.
点评 本题主要考查三角恒等变换,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
3.某程序框图如图所示,运行该程序,那么输出k的值是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( )
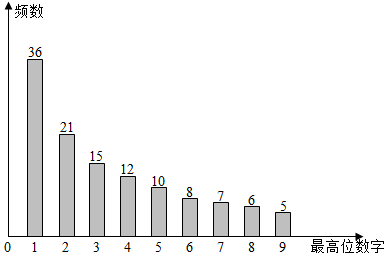

| A. | P=lg(1+$\frac{1}{d}$) | B. | P=$\frac{1}{d+2}$ | C. | P=$\frac{{(d-5)}^{2}}{120}$ | D. | P=$\frac{3}{5}$×$\frac{1}{{2}^{d}}$ |
18.已知函数f(x)=$\left\{\begin{array}{l}{sin(2x+\frac{π}{3})(x≥0)}\\{cos(ωx+φ)(x<0)}\end{array}\right.$(其中ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$).若对于任意的x均有f(x-$\frac{π}{6}$)=f($\frac{π}{3}$-x),则sin(ωφ)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
3.等差数列{an}中,若a1+a9=4,则a5等于( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |