题目内容
15.设向量$\overrightarrow{AB}$=(3,4),$\overrightarrow{BC}$=(-2,-1),则cos∠BAC等于( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由已知向量的坐标求出$\overrightarrow{AC}$的坐标,再求出$|\overrightarrow{AB}|、|\overrightarrow{AC}|$及$\overrightarrow{AB}•\overrightarrow{AC}$,代入数量积求夹角公式得答案.
解答 解:∵$\overrightarrow{AB}$=(3,4),$\overrightarrow{BC}$=(-2,-1),
∴$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=(3,4)+(-2,-1)=(1,3)$,
∴$|\overrightarrow{AB}|=\sqrt{{3}^{2}+{4}^{2}}=5$,$|\overrightarrow{AC}|=\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$,$\overrightarrow{AB}•\overrightarrow{AC}$=3×1+4×3=15,
∴cos∠BAC=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{15}{5×\sqrt{10}}=\frac{3\sqrt{10}}{10}$.
故选:B.
点评 本题考查平面向量的数量积运算,考查了由数量积求斜率的夹角,是中档题.

练习册系列答案
相关题目
3.等差数列{an}中,若a1+a9=4,则a5等于( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
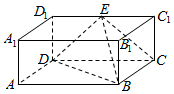 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,