题目内容
8.已知△ABC的内角A,B,C的对边分别为a,b,c,且满足2cos C(a cos B+b cos A )=c.①求C;
②若c=$\sqrt{7}$,ab=6.
求△ABC的周长.
分析 ①根据正弦定理可得cosC=$\frac{1}{2}$,即可求出C,
②根据余弦定理即可求出a+b的值,即可得到三角形的周长.
解答 解:①∵2cosC(acosB+bcosA)=c
由正弦定理得2cosC(sinAcosB+sinBcosA)=sinC,
∴2cosCsin(A+B)=sinC,
∴2cosCsinC=sinC,
∵C∈(0,π),
∴sinC≠0,
∴cosC=$\frac{1}{2}$,
∴C=$\frac{π}{3}$;
②由余弦定理得c2=a2+b2-2abcosC,
∴7=a2+b2-ab=(a+b)2-3ab═(a+b)2-18,
解得a+b=5或a+b=-5(舍),
∴a+b=5,
∴△ABC的周长为a+b+c=5+$\sqrt{7}$.
点评 本题考查了正弦定理和余弦定理,考查了学生的运算能力,属于中档题.

练习册系列答案
相关题目
19.已知命题p:f(x)=lnx+2x2+6mx+1在(0,+∞)上单调递增,q:m≥-5,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
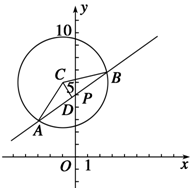 已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.
已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.