题目内容
10.如果(1-2x)7=a0+a1x+a2x2+…+a7x7.(1)求a0.
(2)那么a0+a1+a2+…+a7的值等于多少.
分析 (1)在所给的等式中,令x=0,可得a0的值.
(2)在所给的等式中,令x=1,可得a0+a1+a2+…+a7的值.
解答 解:(1)∵(1-2x)7=a0+a1x+a2x2+…+a7x7 ,令x=0,可得a0=1.
(2)在等式(1-2x)7=a0+a1x+a2x2+…+a7x7 中,令x=1,
可得a0+a1+a2+…+a7=-1.
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
相关题目
7.某几何体的三视图如图所示,则该几何体的体积为( )
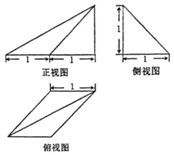

| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
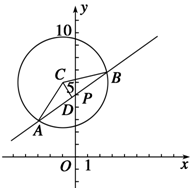 已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.
已知圆C过P(2,6),Q(-2,2)两点,且圆心C在直线3x+y=0上.