题目内容
判断下列命题的真假.
(1)?x∈R,都有x2-x+1>
;
(2)?α,β使cos(α-β)=cosα-cosβ;
(3)?x,y∈N,都有x-y∈N;
(4)?x0,y0∈Z,使得
x0+y0=3.
(1)?x∈R,都有x2-x+1>
| 1 |
| 2 |
(2)?α,β使cos(α-β)=cosα-cosβ;
(3)?x,y∈N,都有x-y∈N;
(4)?x0,y0∈Z,使得
| 2 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1利用x2-x+1=(x-
)2+
>
可判断(1);
(2)令α=
,β=
,满足cos(α-β)=cosα-cosβ,可判断(2);
(3令x=1,y=5,x-y=-4∉N,可判断(3);
(4)?x0=0,y0=3∈Z,使得
x0+y0=3,可判断(4).
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
(2)令α=
| π |
| 4 |
| π |
| 2 |
(3令x=1,y=5,x-y=-4∉N,可判断(3);
(4)?x0=0,y0=3∈Z,使得
| 2 |
解答:
解:(1)真命题,∵x2-x+1=(x-
)2+
≥
>
.…(3分)
(2)真命题,如α=
,β=
,符合题意.…(6分)
(3)假命题,例如x=1,y=5,但x-y=-4∉N.…(9分)
(4)真命题,例如x0=0,y0=3符合题意.…(12分)
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
(2)真命题,如α=
| π |
| 4 |
| π |
| 2 |
(3)假命题,例如x=1,y=5,但x-y=-4∉N.…(9分)
(4)真命题,例如x0=0,y0=3符合题意.…(12分)
点评:本题考查命题的真假判断,考查全称命题与特称命题的概念及应用,属于基本知识的考查.

练习册系列答案
相关题目
不等式x2-4x-5<0的解集是( )
| A、(-1,5) |
| B、(-∞,-1)∪(5,+∞) |
| C、(0,5) |
| D、(-1,0) |
设集合A={x|x2-3x<0},集合B={y|y=2x,0≤x≤1},则A∩B=( )
| A、(0,1] |
| B、(0,2] |
| C、[1,2] |
| D、[1,3) |
已知f(x)=
则f[f(
)]的值为( )
|
| 2 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
 如图,在正四面体A-BCD中,E为棱AD的中点,则CE与平面BCD的夹角的正弦值为( )
如图,在正四面体A-BCD中,E为棱AD的中点,则CE与平面BCD的夹角的正弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若一条直线与两个平行平面中的一个平面平行,则这条直线与另一个平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
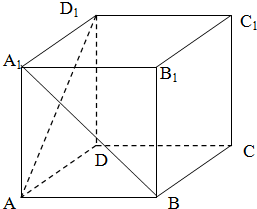 已知正方体ABCD-A1B1C1D1,求:
已知正方体ABCD-A1B1C1D1,求: