题目内容
3.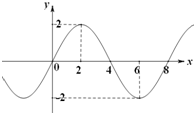 函数f(x)=Asin(ωx+ϕ)(其中A>0,ω>0)的部分图象如图所示,则f(2)+f(3)+…+f(2016)的值为( )
函数f(x)=Asin(ωx+ϕ)(其中A>0,ω>0)的部分图象如图所示,则f(2)+f(3)+…+f(2016)的值为( )| A. | $\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | 0 | D. | $-\sqrt{2}$ |
分析 求出f(x)的解析式,根据函数图象的对称性可知f(x)在1个周期内的连续整数对于的函数值之和为0,故而f(0)+f(1)+f(2)+…+f(2016)=0,从而得出答案.
解答 解:由函数图象可知f(x)的周期为8,A=2,φ=0.∴ω=$\frac{2π}{8}=\frac{π}{4}$.
∴f(x)=2sin$\frac{π}{4}$x.
由f(x)的对称性可知在一个周期内f(0)+f(1)+f(2)+…+f(8)=0,
而[0,2016]恰好为252个周期,∴f(0)+f(1)+f(2)+…+f(2016)=0.
∴f(2)+f(3)+…+f(2016)=-f(0)-f(1).
∵f(0)=0,f(1)=2sin$\frac{π}{4}$=$\sqrt{2}$,
∴-f(0)-f(1)=-$\sqrt{2}$.
故选:D.
点评 本题考查了正弦函数的图象与性质,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
14.在边长为8的正方形ABCD内任取一点M,则∠AMB>90°的概率为( )
| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
11.数列1,-4,9,-16,25…的一个通项公式为( )
| A. | an=n2 | B. | an=(-1)nn2 | C. | an=(-1)n+1n2 | D. | an=(-1)n(n+1)2 |
8.为了检查一批光盘的质量,从中抽取了500张进行检测,则这个问题中的样本容量是( )
| A. | 500张光盘 | B. | 500 | C. | 500张光盘的质量 | D. | 光盘的全体 |
12.已知z∈C,|z-(1+i)|=1,则|z+2+3i|的最大值为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |