题目内容
15．设f（x）=x3-$\frac{1}{2}$x2-2x+5，若至少存在一个x0∈[-1，2]时，f（x0）＜m成立，则实数m的取值范围是m＞$\frac{7}{2}$．分析 由题意可得：m＞f（x）min，利用导数研究函数的单调性极值与最值即可得出．
解答 解：至少存在一个x0∈[-1，2]时，f（x0）＜m成立，∴m＞f（x）min．
| x | $[-1，-\frac{2}{3}）$ | $-\frac{2}{3}$ | $（-\frac{2}{3}，1）$ | 1 | （1，2] |
| f′（x） | + | 0 | - | 0 | + |
| f（x） | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
列表如下：由表格可知：x=1时，函数f（x）取得极小值，f（1）=1-$\frac{1}{2}$-2+5=$\frac{7}{2}$，又f（-1）=-1-$\frac{1}{2}$+2+5=$\frac{15}{2}$．
∴f（x）min=$\frac{7}{2}$．
∴$m＞\frac{7}{2}$．
故答案为：$m＞\frac{7}{2}$．
点评 本题考查了微积分基本定理、二项式定理的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．已知函数$f（x）=\frac{1}{{\sqrt{x+2}}}+{（x-1）^0}$的定义域为M，g（x）=ln（2-x）的值域为N，则M∩N=（ ）
| A． | {x|x＞-2} | B． | {x|x＜2} | C． | {x|-2＜x＜2} | D． | {x|x＞-2，x≠1} |
6．把函数y=sinx（x∈R）的图象上所有的点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再把所得图象向左平行移动$\frac{π}{6}$个单位长度，得到的图象所表示的函数是（ ）
| A． | y=sin（$\frac{1}{2}$x+$\frac{π}{6}}$），x∈R | B． | y=sin（$\frac{1}{2}$x+$\frac{π}{12}$），x∈R | ||
| C． | y=sin（2x+$\frac{π}{3}$），x∈R | D． | y=sin（2x+$\frac{π}{6}$），x∈R |
3．
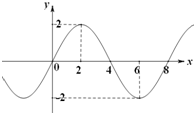函数f（x）=Asin（ωx+ϕ）（其中A＞0，ω＞0）的部分图象如图所示，则f（2）+f（3）+…+f（2016）的值为（ ）
函数f（x）=Asin（ωx+ϕ）（其中A＞0，ω＞0）的部分图象如图所示，则f（2）+f（3）+…+f（2016）的值为（ ）| A． | $\sqrt{2}$ | B． | $2+\sqrt{2}$ | C． | 0 | D． | $-\sqrt{2}$ |
20．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一周期内的图象时，列表并填入了部分数据，如下表：
（1）请将上表空格中的数据在答卷的相应位置上，并求函数f（x）的解析式；
（2）若y=f（x）的图象上所有点向左平移$\frac{π}{6}$个单位后对应的函数为g（x），求当x∈[-$\frac{π}{4}$，$\frac{π}{4}$]时，函数y=g（x）的值域．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{7π}{12}$ | |||
| Asin（ωx+φ） | 3 | 0 |
（2）若y=f（x）的图象上所有点向左平移$\frac{π}{6}$个单位后对应的函数为g（x），求当x∈[-$\frac{π}{4}$，$\frac{π}{4}$]时，函数y=g（x）的值域．