题目内容
18．下列函数求导运算正确的个数为（ ）①（3x）′=3xlog3e；②（log2x）′=$\frac{1}{xln2}$；③（ex）′=ex；④（x•ex）′=ex+1．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据导数的运算法则和导数的基本公式计算后即可判断．
解答 解：①（3x）′=3xln3；故①错误，
②（log2x）′=$\frac{1}{xln2}$；故②正确，
③（ex）′=ex；故③正确，
④（x•ex）′=ex+x•ex．故错误．
故正确的个数有2个，
故选：B．
点评 本题考查了导数的运算法则，属于基础题．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
9．若$\frac{cos2α}{sin（α+\frac{π}{4}）}$=-$\frac{2\sqrt{5}}{5}$，且α∈（$\frac{π}{4}$，$\frac{π}{2}$），则tan2α的值是（ ）
| A． | -$\frac{4}{3}$ | B． | -$\frac{3}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
6．把函数y=sinx（x∈R）的图象上所有的点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），再把所得图象向左平行移动$\frac{π}{6}$个单位长度，得到的图象所表示的函数是（ ）
| A． | y=sin（$\frac{1}{2}$x+$\frac{π}{6}}$），x∈R | B． | y=sin（$\frac{1}{2}$x+$\frac{π}{12}$），x∈R | ||
| C． | y=sin（2x+$\frac{π}{3}$），x∈R | D． | y=sin（2x+$\frac{π}{6}$），x∈R |
13．计算：cos25°sin55°-cos65°cos55°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
3．
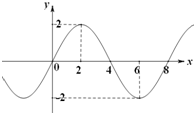函数f（x）=Asin（ωx+ϕ）（其中A＞0，ω＞0）的部分图象如图所示，则f（2）+f（3）+…+f（2016）的值为（ ）
函数f（x）=Asin（ωx+ϕ）（其中A＞0，ω＞0）的部分图象如图所示，则f（2）+f（3）+…+f（2016）的值为（ ）| A． | $\sqrt{2}$ | B． | $2+\sqrt{2}$ | C． | 0 | D． | $-\sqrt{2}$ |