题目内容
3.已知函数f(x)=cosωx-sinωx(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,则ω的取值不可能为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 利用两角和的余弦公式化简函数的解析式,再利用余弦函数的单调性求得f(x)的减区间,结合条件可得,-$\frac{π}{4ω}$≤-$\frac{π}{2}$,且 $\frac{3π}{4ω}$≥$\frac{π}{2}$,由此求得ω的范围,从而得出结论.
解答 解:∵函数f(x)=cosωx-sinωx=$\sqrt{2}$cos(ωx+$\frac{π}{4}$)(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,
∴2kπ≤ωx+$\frac{π}{4}$<≤2kπ+π,求得-$\frac{π}{4ω}$+$\frac{2kπ}{ω}$≤x≤$\frac{3π}{4ω}$+$\frac{2kπ}{ω}$ (k∈Z).
∵f(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,∴-$\frac{π}{4ω}$≤-$\frac{π}{2}$,且 $\frac{3π}{4ω}$≥$\frac{π}{2}$,
求得 0<ω≤$\frac{1}{2}$,
故选:D.
点评 本题主要考查两角和的余弦公式,余弦函数的单调性,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
14.如图,在正方形ABCD中,AD=4,E为DC上一点,且$\overrightarrow{DE}$=3$\overrightarrow{EC}$,则$\overrightarrow{AB}$•$\overrightarrow{AE}$( )
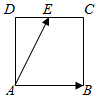

| A. | 20 | B. | 16 | C. | 15 | D. | 12 |
11.下列判断错误的是( )
| A. | 命题“若am2≤bm2,则a≤b”是假命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x0∈R,${{x}_{0}}^{3}$-${{x}_{0}}^{2}$-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 命题“p∨q为真命题”是命题“p∧q为真”的充分不必要条件 |
8.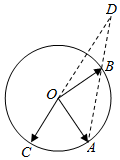 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |