题目内容
18.在半径为r的圆O上的弓形中,底AB=$\sqrt{2}$r,C为劣弧$\widehat{AB}$上的一点,且CD⊥AB,D为垂足,点C圆O上运动,问点C在什么位置时,△ADC的面积有最大值?分析 先表示出△ACD的面积,再用基本不等式求出最大面积.
解答 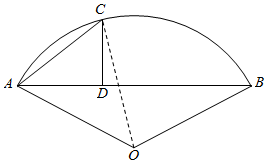 解:∵半径为r的圆O上的弓形中,底AB=$\sqrt{2}$r,
解:∵半径为r的圆O上的弓形中,底AB=$\sqrt{2}$r,
∴∠AOB=90°.
连接OC,设∠CAB=α,则∠BOC=2α,∠AOC=90°-2α,
∴AC=2rsin(45°-α),
∴AD=ACcosα,
∴△ACD的面积S=$\frac{1}{2}×AC×AD×sinα$=r2sin2(45°-α)sin2α
=$\frac{{r}^{2}}{2}×(1-sin2α)sin2α$≤$\frac{{r}^{2}}{2}×(\frac{1}{2})^{2}$=$\frac{{r}^{2}}{8}$.
当且仅当1-sin2α=sin2α,即sin2α=$\frac{1}{2}$,
∴α=$\frac{π}{12}$时,△ACD的面积最大,最大面积为$\frac{{r}^{2}}{8}$.
点评 本题考查三角形面积的计算,考查三角函数知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.已知集合A={x|2x-1<1},B=(-2,2],则A∩B=( )
| A. | (-2,0) | B. | (-2,2] | C. | (1,2] | D. | (-2,1) |
3.若实数x,y满足不等式组$\left\{\begin{array}{l}{2x-3y+6≥0}\\{4x-y-8≤0}\\{x+y-2≥0}\end{array}\right.$,则z=x-y的最大值为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
10.已知等差数列{an}的前n项和为Sn,且S10=5,a7=1,则a1=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
7.已知集合A={x|(x-4)(x+2)<0},B={-3,-1,1,3,5},则A∩B=( )
| A. | {-1,1,3} | B. | {-3,-1,1,3} | C. | {-1,1,3,5} | D. | {-3,5} |
8.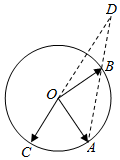 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |