题目内容
11.有命题m:“?x0∈(0,$\frac{1}{3}$),($\frac{1}{2}$)${\;}^{{x}_{0}}$<log${\;}_{\frac{1}{3}}$x0”,n:“?x0∈(0,+∞),($\frac{1}{2}$)${\;}^{{x}_{0}}$=log${\;}_{\frac{1}{3}}$x0>x0”,则在命题p1:m∨n,p2:m∧n,p3:(¬m)∨n和p4:m∧(¬n)中,真命题是( )| A. | p1,p2,p3 | B. | p2,p3,p4 | C. | p1,p3 | D. | p2,p4 |
分析 命题m:利用指数函数与对数函数的大小与1比较即可得出大小关系;命题n:利用指数函数与对数函数的图象与单调性即可得出大小关系.再利用复合命题真假的判定方法即可判断出.
解答 解:命题m:“?x0∈(0,$\frac{1}{3}$),($\frac{1}{2}$)${\;}^{{x}_{0}}$<1<log${\;}_{\frac{1}{3}}$x0”,因此是真命题;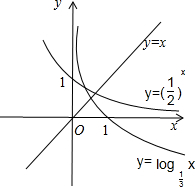
命题n:“?x0∈(0,+∞),($\frac{1}{2}$)${\;}^{{x}_{0}}$=log${\;}_{\frac{1}{3}}$x0>x0”,如图所示,因此是真命题.
则在命题p1:m∨n,p2:m∧n,p3:(¬m)∨n和p4:m∧(¬n)中,
真命题是p11,p2,p3是真命题,p4是假命题.
故选:A.
点评 本题考查了简易逻辑的判定、指数函数与对数函数的性质,考查了数形结合的方法、推理能力与计算能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
1.要得到函数y=3sin2x的图象,只需将函数y=3sin(2x-$\frac{π}{3}$)的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
2.若集合M={x|x≤6},a=$\sqrt{5}$,则下列结论正确的是( )
| A. | {a}⊆M | B. | a⊆M | C. | {a}∈M | D. | a∉M |
6.函数y=$tan(2x-\frac{π}{4})$的其中一个对称中心为( )
| A. | $(-\frac{π}{8},0)$ | B. | $(\frac{π}{2},0)$ | C. | (0,0) | D. | $(\frac{π}{4},0)$ |
3.命题p:“非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,若$\overrightarrow{a}$•$\overrightarrow{b}$<0,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为钝角”,命题q:“对函数f(x),若f′(x0)=0,则x=x0为函数的极值点”,则下列命题中真命题是( )
| A. | p∧q | B. | p∨q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
20.在△ABC中,“sin A>sin B”是“A>B”的( )条件.
| A. | 充分必要 | B. | 充分不必要 | C. | 必要不充分 | D. | 不充分不必要 |