题目内容
19.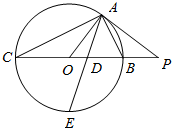 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.(1)求证:$\frac{AB}{AC}=\frac{PA}{PC}$.
(2)求AD•AE的值.
分析 (1)由弦切角定理推导出△PAB~△PCA,由此能证明$\frac{AB}{AC}=\frac{PA}{PC}$.
(2)由切割线定理得PA2=PB•PC,由AE是∠BAC的角平分线,得△AEC~△ABD,由此能求出AD•AE的值.
解答  证明:(1)∵PA为圆O的切线,∴∠PAB=∠ACP,
证明:(1)∵PA为圆O的切线,∴∠PAB=∠ACP,
又∠P为公共角,∴△PAB~△PCA,
∴$\frac{AB}{AC}=\frac{PA}{PC}$(4分)
解:(2)∵PA为圆O的切线,BC是过点O的割线,
∴PA2=PB•PC,∴PC=40,BC=30,
又∠CAB=90°,∴AC2+AB2=BC2=900,
又由(1)知$\frac{AB}{AC}=\frac{PA}{PC}=\frac{1}{2}$,∴$AC=12\sqrt{5}$,$AB=6\sqrt{5}$,
∵AE是∠BAC的角平分线,且∠AEC=∠ABD,∴△AEC~△ABD,
∴$\frac{AB}{AE}=\frac{AD}{AC}$,
∴$AD•AE=AB•AC=6\sqrt{5}×12\sqrt{5}=360$.(10分)
点评 本题考查两组线段比值相等的证明,考查两线段乘积的求法,是中档题,解题时要认真审题,注意弦切角定理和切割线定理的合理运用.

练习册系列答案
相关题目
7.设集合A={x|8-2x>0},集合B={x|x=2n-1,n∈N*},则A∩B等于( )
| A. | {-1,1} | B. | {-1,3} | C. | {3,1,-1} | D. | {1,3} |
14.若函数f(x)=$\frac{x+a}{{e}^{x}}$在区间(-∞,2)上为单调递增函数,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (0,e] | C. | (-∞,-1] | D. | (-∞,-e) |
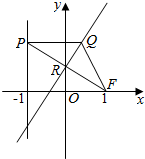 在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.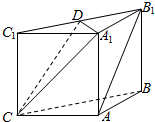 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90°,点D是棱B1C1的中点.