题目内容
8.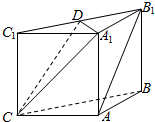 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90°,点D是棱B1C1的中点.(1)求证:A1D⊥平面BB1C1C;
(2)求证:AB1∥平面A1DC;
(3)求三棱锥C1-A1CD的体积.
分析 (1)先证明AA1⊥平面ABC,可得CC1⊥AD,再利用线面垂直的判定定理,即可证明AD⊥平面BCC1B1;
(2)利用三角形中位线的性质,证明A1B∥OD,利用线面平行的判定定理证明A1B∥平面AC1D;
(3)利用等体积转化法求解三棱锥C1-A1CD的体积即可.
解答 (1)证明:AC∩AB=A,侧面ABB1A1,ACC1A1均为正方形,
AC∩AB=A,
AC,AB?平面ABC,∴AA1⊥平面ABC.
∵AA1∥CC1,∴CC1⊥平面ABC,∴平面平面BB1C1C⊥平面ABC,…(2分)
∴平面平面BB1C1C⊥平面A1B1C1,D是B1C1中点,AB=AC=1,
∴A1D⊥B1C1
∴A1D⊥平面BB1C1C;…(5分)
(2)证明:连结A1C,交AC1于点O,连结OD,
因为ACC1A1为正方形,所以O为AC1中点,
又D为BC中点,所以OD为△A1BC中位线,
所以A1B∥OD,…(6分)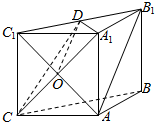
因为OD?平面AC1D,AB1?平面AC1D,
所以A1B∥平面AC1D…(8分)
(3)由(1)可知A1A三棱柱ABC-A1B1C1的高 …(9分)
侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90°,点D是棱B1C1的中点,${V_{{C_1}-{A_1}CD}}={V_{C-{A_1}{C_1}D}}=\frac{1}{3}{S_{△{A_1}{C_1}D}}•C{C_1}=\frac{1}{3}×\frac{1}{4}×1=\frac{1}{12}$…(10分),
即三棱锥C1-A1CD的体积为:$\frac{1}{12}$.…(12分)
点评 本题考查几何体的体积的求法,直线与平面平行与垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
16.下面关于命题“p:所有抛物线的离心率为1”的说法正确的是( )
| A. | p是特称命题,¬p:存在一条抛物线的离心率不为1 | |
| B. | p是特称命题,¬p:存在一条抛物线的离心率为1 | |
| C. | p是全称命题,¬p:存在一条抛物线的离心率不为1 | |
| D. | p是全称命题,¬p:存在一条抛物线的离心率为1 |
3.已知直线l的方程为x-my+2=0,则直线l( )
| A. | 恒过点(-2,0)且不垂直x轴 | B. | 恒过点(-2,0)且不垂直y轴 | ||
| C. | 恒过点(2,0)且不垂直x轴 | D. | 恒过点(2,0)且不垂直y轴 |
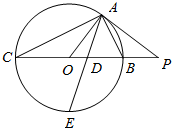 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E. 已知圆C:x2-(1+a)x+y2-ay+a=0(a∈R).
已知圆C:x2-(1+a)x+y2-ay+a=0(a∈R).