题目内容
7.设集合A={x|8-2x>0},集合B={x|x=2n-1,n∈N*},则A∩B等于( )| A. | {-1,1} | B. | {-1,3} | C. | {3,1,-1} | D. | {1,3} |
分析 求出A中不等式的解集确定出A,求出B中x的值确定出B,找出两集合的交集即可.
解答 解:由A中不等式解得:x<4,即A=(-∞,4),
由B中x=2n-1,n∈N*,得到B={1,3,5,…}(从1开始的连续奇数),
则A∩B={1,3},
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知数列{an}中a1=1,an+1=$\frac{a_n}{{3{a_n}+1}}$,则a34=( )
| A. | $\frac{34}{103}$ | B. | 100 | C. | $\frac{1}{100}$ | D. | $\frac{1}{104}$ |
16.下面关于命题“p:所有抛物线的离心率为1”的说法正确的是( )
| A. | p是特称命题,¬p:存在一条抛物线的离心率不为1 | |
| B. | p是特称命题,¬p:存在一条抛物线的离心率为1 | |
| C. | p是全称命题,¬p:存在一条抛物线的离心率不为1 | |
| D. | p是全称命题,¬p:存在一条抛物线的离心率为1 |
 《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )
《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )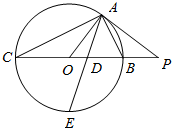 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E. 已知圆C:x2-(1+a)x+y2-ay+a=0(a∈R).
已知圆C:x2-(1+a)x+y2-ay+a=0(a∈R).