题目内容
4.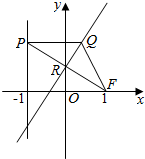 在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
在平面直角坐标系xoy中,设点F(1,0),直线l:x=-1,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.(1)求动点Q的轨迹的方程.
(2)记Q的轨迹的方程为E,曲线E与直线y=kx-2相交于不同的两点A,B,且弦AB中点的纵坐标为2,求k的值.
分析 (1)求出直线l的方程.利用点R是线段FP的中点,且RQ⊥FP,|PQ|是点Q到直线l的距离.然后求出动点Q的轨迹方程.
(2)(法一)设A(x1,y1),B(x2,y2),联立$\left\{{\begin{array}{l}{y=kx-2}\\{{y^2}=4x}\end{array}}\right.$消去x,利用韦达定理以及中点坐标个数,求出k即可.
(法二)设A(x1,y1),B(x2,y2),利用平方差法求解即可.
解答 解:(1)依题意知,直线l的方程为:x=-1.点R是线段FP的中点,且RQ⊥FP,
∴RQ是线段FP的垂直平分线-----(1分)
∴|PQ|是点Q到直线l的距离.
∵点Q在线段FP的垂直平分线,∴|PQ|=|QF|-----(3分)
故动点Q的轨迹E是以F为焦点,l为准线的抛物线,其方程为:y2=4x(x>0)-----(5分)
(2)(法一)设A(x1,y1),B(x2,y2),依题意知,k≠0,由$\left\{{\begin{array}{l}{y=kx-2}\\{{y^2}=4x}\end{array}}\right.$有,$y=k\frac{y^2}{4}-2$
即ky2-4y-8=0,-----(7分)
∴${y_1}+{y_2}=\frac{4}{k}$,-----(8分)
又$\frac{{{y_1}+{y_2}}}{2}=2$,∴k=1-----(10分)
又当k=1时,△=16+32k>0,所以k=1满足题意,-----(11分)
∴k的值是1-----(12分)
(法二)设A(x1,y1),B(x2,y2),则$\left\{{\begin{array}{l}{{y_1}^2=4{x_1}}\\{{y_2}^2=4{x_2}}\end{array}}\right.$,-----(6分)
两式相减有${y_1}^2-{y_2}^2=4({x_1}-{x_2})$,
∴$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{4}{{{y_1}+{y_2}}}$,-----(9分)
又$k=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}},\frac{{{y_1}+{y_2}}}{2}=2$,-----(11分)
则k=1-----(12分)
点评 本题考查抛物线的简单性质的应用,直线与抛物线的位置关系的应用,考查转化思想以及计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | p是特称命题,¬p:存在一条抛物线的离心率不为1 | |
| B. | p是特称命题,¬p:存在一条抛物线的离心率为1 | |
| C. | p是全称命题,¬p:存在一条抛物线的离心率不为1 | |
| D. | p是全称命题,¬p:存在一条抛物线的离心率为1 |
 《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )
《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )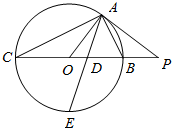 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.