题目内容
11.点A(-2,3)关于直线l:3x-y-1=0的对称点坐标是(4,1).分析 设所求对称点的坐标为(a,b),由对称性可得$\left\{\begin{array}{l}{\frac{b-3}{a+2}•3=-1}\\{3•\frac{a-2}{2}-\frac{b+3}{2}-1=0}\end{array}\right.$,解方程组可得.
解答 解:设所求对称点的坐标为(a,b),
则$\left\{\begin{array}{l}{\frac{b-3}{a+2}•3=-1}\\{3•\frac{a-2}{2}-\frac{b+3}{2}-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=4}\\{b=1}\end{array}\right.$,
∴所求对称点的坐标为(4,1),
故答案为:(4,1).
点评 本题考查点与直线的对称性,涉及中点公式和直线的垂直关系,属基础题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
16.下面关于命题“p:所有抛物线的离心率为1”的说法正确的是( )
| A. | p是特称命题,¬p:存在一条抛物线的离心率不为1 | |
| B. | p是特称命题,¬p:存在一条抛物线的离心率为1 | |
| C. | p是全称命题,¬p:存在一条抛物线的离心率不为1 | |
| D. | p是全称命题,¬p:存在一条抛物线的离心率为1 |
3.已知直线l的方程为x-my+2=0,则直线l( )
| A. | 恒过点(-2,0)且不垂直x轴 | B. | 恒过点(-2,0)且不垂直y轴 | ||
| C. | 恒过点(2,0)且不垂直x轴 | D. | 恒过点(2,0)且不垂直y轴 |
1.集合A={1,2},B={1,2,3},则下列关系正确的是( )
| A. | A=B | B. | A∩B=∅ | C. | A⊆B | D. | A?B |
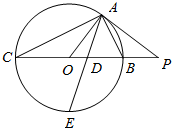 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.