Question

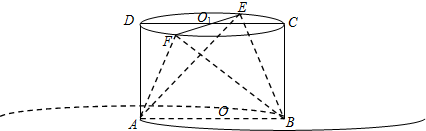
如图，在△ABC中，BC=2，BC边上的高AD=1，P是BC边上任一点，PE∥AB交AC于点E，PF∥AC交AB于点F．
（1）设BP=x，请写出用x表示S_△PEF的表达式；
（2）P在BC的什么位置时，S_△PEF取得最大值？

Answer 1

考点：函数解析式的求解及常用方法,函数的最值及其几何意义

专题：函数的性质及应用

分析：（1）首先，求解三角形ABC的面积，然后结合三角形相似，面积比等于相似比的平方，得到△CEP和△BPF的面积，再根据四边形AEPF为平行四边形，从而得到S_△PEF的表达式；
（2）根据（1），结合二次函数的性质，求解最大值即可．

解答： 解：（1）∵BC=2，BC边上的高AD=1，
∴S△ABC=

1

2

×2×1=1，
∵BP=x，
∴PC=2-x，
∵PE∥AB，
∴△CEP与△CAB相似，
∴

S△CEP

S△CAB

=(

2-x

2

)2，
∴S△CEP=1-x+

x2

4

，
同理，得到S△BPF=

x2

4

，
∵四边形AEPF为平行四边形，
∴S_△PEF=

1

2

S?AEPF=

1

2

（S_△ABC-S_△CEP-S_△BPF）
=-

1

4

x2+

1

2

x，（0＜x＜2）．
S_△PEF=-

1

4

x2+

1

2

x（0＜x＜2）．
（2）由（1）知S_△PEF=-

1

4

x2+

1

2

x=-

1

4

（x-1）²+

1

4

，
∵0＜x＜2，
∴当x=1时，面积有最大值

1

4

．

点评：本题结合平面几何知识综合考查建立函数解析式的能力，找准变量之间的关系是解题的关键，属于难题．