题目内容
已知三棱柱ABC-A1B1C1的三视图及直观图如图所示,根据图中所给数据,解答下列问题:

(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)试在棱CC1(不包含端点C、C1)上确定一点E的位置,使得EA⊥EB1;
(Ⅲ)求三棱柱ABC-A1B1C1的体积.

(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)试在棱CC1(不包含端点C、C1)上确定一点E的位置,使得EA⊥EB1;
(Ⅲ)求三棱柱ABC-A1B1C1的体积.
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)根据线面垂直的判定定理即可证明C1B⊥平面ABC;
(Ⅱ)根据线面垂直的性质,结合直角三角形的边长关系即可确定E的位置;
(Ⅲ)根据三棱柱ABC-A1B1C1的体积公式即可得到结论..
(Ⅱ)根据线面垂直的性质,结合直角三角形的边长关系即可确定E的位置;
(Ⅲ)根据三棱柱ABC-A1B1C1的体积公式即可得到结论..
解答:
解:(Ⅰ)由三视图可知AB⊥侧面BB1C1C,
则AB⊥BC1,
∵BC=1,CC1=BB1=2,∠BCC1=
,
在△BC1C中,由余弦定理得BC1=
,故有BC2+BC12=CC12,
∴C1B⊥BC,
∵BC∩AB=B,且AB,BC?平面ABC,
∴C1B⊥平面ABC;
(Ⅱ)由EA⊥EB1,AB⊥EB1,AB∩AE=A,
AE,AB?平面ABE,从而B1E⊥平面ABE;且BE?平面ABE,
故B1E⊥BE,设CE=x,则C1E=2-x,
则BE2=1+x2-x,
∵∠B1C1C=
,∴B1E2=x2-5x+7,
Rt△BEB1中,x2-5x+7+1+x2-x=4,解得x=1或x=2.
故E是CC1的中点时,有EA⊥EB1;
(Ⅲ)由(Ⅱ)知S△ABC=
BC•AB=
×1×
=
,
由(Ⅰ)知C1B⊥平面ABC,BC1=
,
∴三棱柱ABC-A1B1C1的体积V=3VA-CBC1=3×
S△CBC1•AB=
×2×1×sin
×
=
.
则AB⊥BC1,
∵BC=1,CC1=BB1=2,∠BCC1=
| π |
| 3 |
在△BC1C中,由余弦定理得BC1=
| 3 |
∴C1B⊥BC,
∵BC∩AB=B,且AB,BC?平面ABC,
∴C1B⊥平面ABC;
(Ⅱ)由EA⊥EB1,AB⊥EB1,AB∩AE=A,
AE,AB?平面ABE,从而B1E⊥平面ABE;且BE?平面ABE,
故B1E⊥BE,设CE=x,则C1E=2-x,
则BE2=1+x2-x,
∵∠B1C1C=
| 2π |
| 3 |
Rt△BEB1中,x2-5x+7+1+x2-x=4,解得x=1或x=2.
故E是CC1的中点时,有EA⊥EB1;
(Ⅲ)由(Ⅱ)知S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
由(Ⅰ)知C1B⊥平面ABC,BC1=
| 3 |
∴三棱柱ABC-A1B1C1的体积V=3VA-CBC1=3×
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 2 |
| ||
| 2 |
点评:本题主要考查线面垂直的判断以及三棱柱的体积的计算,要求熟练掌握空间线面垂直的判定定理和三棱锥的体积公式.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
设集合A={x|(x+1)(x-5)>0},B={x|a<x<a+8},若A∪B=R,则实数a的取值范围是( )
| A、-3<a<-1 |
| B、-3≤a≤-1 |
| C、a≤-3或a≥-1 |
| D、a<-3或a>-1 |
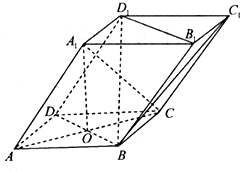 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC,BD交于点O,A1O⊥平面ABCD,A1A=BD=2,AC=2 已知正方体ABCD-A1B1C1D1,求证:
已知正方体ABCD-A1B1C1D1,求证: