题目内容
设F1,F2分别为椭圆
+y2=1的左、右焦点,斜率为k的直线l经过右焦点F2,且与椭圆相交于A,B两点,且△ABF1的周长为4
.
(Ⅰ)求椭圆的方程;
(Ⅱ)如果△ABF1的重心在y轴上,求直线l的斜率k.
| x2 |
| a2 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)如果△ABF1的重心在y轴上,求直线l的斜率k.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由△ABF1的周长为4
,知4a=4
,由此能求出椭圆的方程.
(Ⅱ)直线l:y=k(x-1),联立
,得(1+2k2)x2-4k2x+2k2-2=0,由此利用韦达定理、根的判别式和三角形重心坐标公式能求出直线l的斜率.
| 2 |
| 2 |
(Ⅱ)直线l:y=k(x-1),联立
|
解答:
解:(Ⅰ)∵F1,F2分别为椭圆
+y2=1的左、右焦点,
斜率为k的直线l经过右焦点F2,且与椭圆相交于A,B两点,
且△ABF1的周长为4
,
∴4a=4
,解得a=
,
∴椭圆的方程为
+y2=1.
(Ⅱ)∵椭圆的方程为
+y2=1,
∴F1(-1,0),F2(1,0),∴直线l:y=k(x-1),
联立
,得(1+2k2)x2-4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),则x1+x2=
,
△=16k4-4(1+2k2)(2k2-2)>0,
∵△ABF1的重心在y轴上,
∴x1+x2-1=
-1=0,
解得k=±
,满足△>0.
∴直线l的斜率k=±
.
| x2 |
| a2 |
斜率为k的直线l经过右焦点F2,且与椭圆相交于A,B两点,
且△ABF1的周长为4
| 2 |
∴4a=4
| 2 |
| 2 |
∴椭圆的方程为
| x2 |
| 2 |
(Ⅱ)∵椭圆的方程为
| x2 |
| 2 |
∴F1(-1,0),F2(1,0),∴直线l:y=k(x-1),
联立
|
设A(x1,y1),B(x2,y2),则x1+x2=
| 4k2 |
| 1+2k2 |
△=16k4-4(1+2k2)(2k2-2)>0,
∵△ABF1的重心在y轴上,
∴x1+x2-1=
| 4k2 |
| 1+2k2 |
解得k=±
| ||
| 2 |
∴直线l的斜率k=±
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查直线的斜率的求法,解题时要认真审题,注意三角形重心坐标公式的合理运用.

练习册系列答案
相关题目
复数z=
的共轭复数是( )
| i |
| 1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若点A(1,m-1,1)和点B(-1,-3,-1)关于原点对称,则m=( )
| A、-4 | B、4 | C、2 | D、-2 |
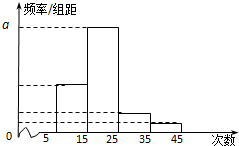 对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,
对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,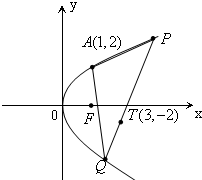 点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点
点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点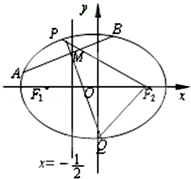 如图,F1,F2是离心率为
如图,F1,F2是离心率为 已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足