题目内容
4.数列{an}的前n项和记为Sn,a1=2,an+1=Sn+2(n∈N*).(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn.
分析 (Ⅰ)由a1=2,an+1=Sn+2(n∈N*),an=Sn-1+2(n≥2),相减利用等比数列的通项公式即可得出.
(Ⅱ)利用“错位相减法”、等比数列的通项公式即可得出.
解答 解:(Ⅰ)由a1=2,an+1=Sn+2(n∈N*),①
an=Sn-1+2(n≥2),②…(2分)
①-②,得$2{a_n}={a_{n+1}}⇒\frac{{{a_{n+1}}}}{a_n}=2$(n≥2).…(4分)
又由a2=S1+2=4,得$\frac{a_2}{a_1}=2$.…(5分)
所以$\frac{{{a_{n+1}}}}{a_n}=2$(n≥1),数列{an}是以2为首项,2为公比的等比数列,故${a_n}={2^n}$.…(6分)
(Ⅱ)由(Ⅰ),得${T_n}=1×2+2×{2^2}+3×{3^3}+…+n×{2^n}$,③
2Tn=1×22+2×33+3×24+…+n×2n+1,④…(8分)
③-④,得$-{T_n}=2+{2^2}+{3^3}+…+{2^n}-n{2^{n+1}}$.…(10分)
所以${T_n}=2+(n-1){2^{n+1}}$.…(12分)
点评 本题考查了“错位相减法”、等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知函数f(x)=x2ex,g(x)=3ex+a(a∈R),若存在x∈[-2,2],使得f(x)>g(x)成立,则a的取值范围是( )
| A. | a>e2 | B. | a<e2 | C. | a>-2e | D. | a<-2e |
19.设函数f(x)=ex(sinx-cosx)(0≤x≤2016π),则函数f(x)的各极大值之和为( )
| A. | $\frac{{{e^π}(1-{e^{2017π}})}}{{1-{e^{2π}}}}$ | B. | $\frac{{{e^π}(1-{e^{1009π}})}}{{1-{e^π}}}$ | ||
| C. | $\frac{{{e^π}(1-{e^{1008π}})}}{{1-{e^{2π}}}}$ | D. | $\frac{{{e^π}(1-{e^{2016π}})}}{{1-{e^{2π}}}}$ |
16.设函数f(x)和g(x)分别是R上的奇函数和偶函数,则函数h(x)=g(x)|f(x)|的图象(( )
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 关于直线y=x对称 |
13.阅读程序框图,如果输出的函数值在区间[1,3]上,则输入的实数x的取值范围是( )
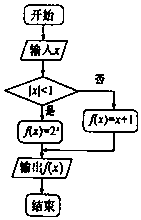

| A. | [0,2] | B. | [0,1] | C. | [-1,1) | D. | (-1,2] |