题目内容
15.已知n=$\int_0^3{({2x-1})dx}$,则${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中x2的系数为1.分析 利用微积分基本定理可得n=$\int_0^3{({2x-1})dx}$=$({x}^{2}-x){|}_{0}^{3}$=6,利用${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中的通项公式:Tk+1=(-1)k•36-k•${∁}_{6}^{k}$${x}^{\frac{5k}{6}-3}$,令$\frac{5k}{6}$-3=2,解得k即可得出.
解答 解:n=$\int_0^3{({2x-1})dx}$=$({x}^{2}-x){|}_{0}^{3}$=6,
则${({\frac{3}{{\sqrt{x}}}-\root{3}{x}})^n}$的展开式中的通项公式:Tk+1=${∁}_{6}^{k}(\frac{3}{\sqrt{x}})^{6-k}(-\root{3}{x})^{k}$=(-1)k•36-k•${∁}_{6}^{k}$${x}^{\frac{5k}{6}-3}$,
令$\frac{5k}{6}$-3=2,解得k=6.
∴x2的系数=$(-1)^{6}×{3}^{0}•{∁}_{6}^{6}$=1.
故答案为:1.
点评 本题考查了二项式定理的应用、微积分基本定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
6.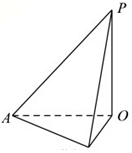 如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
 如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )| A. | 20m | B. | 20$\sqrt{2}$m | C. | 20$\sqrt{3}$m | D. | 40m |
20.在平面直角坐标系中,已知顶点$A(-\sqrt{2},0)$、$B(\sqrt{2},0)$,直线PA与直线PB的斜率之积为$\frac{1}{2}$,则动点P的轨迹方程为( )
| A. | $\frac{x^2}{2}-{y^2}$=1(x≠±$\sqrt{2}$) | B. | $\frac{x^2}{2}-{y^2}$=1 | C. | $\frac{x^2}{2}+{y^2}$=1(y≠0) | D. | $\frac{y^2}{2}+{x^2}$=1 |
7.某校随机调查了110名不同性别的学生每天在校的消费情况,规定:50元以下为正常消费,大于或等于50元为非正常消费.统计后,得到如下的2×2列联表,已知在调查对象中随机抽取1人,为非正常消费的概率为$\frac{3}{11}$.
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,能否有99%的把握认为消费情况与性别有关系?
附临界值表参考公式:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 正常 | 非正常 | 合计 | |
| 男 | 30 | 20 | 50 |
| 女 | 50 | 10 | 60 |
| 合计 | 80 | 30 | 110 |
(Ⅱ)根据列联表的数据,能否有99%的把握认为消费情况与性别有关系?
附临界值表参考公式:
| P(K2≥k0) | 0.100 | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
5.若点A的坐标是(3,2),F是抛物线y2=2x的焦点,点P在抛物线上移动,为使得|PA|+|PF|取得最小值,则P点的坐标是( )
| A. | (1,2) | B. | (2,1) | C. | (2,2) | D. | (0,1) |
 如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).
如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).