在四面体S-ABC中.SA⊥平面ABC.∠ABC=90°.SA=AC=2.AB=1.则该四面体的外接球的表面积为8π．题目和参考答案——青夏教育精英家教网—

题目内容

14．在四面体S-ABC中，SA⊥平面ABC，∠ABC=90°，SA=AC=2，AB=1，则该四面体的外接球的表面积为8π．

分析由题意，SC的中点为球心，计算三棱锥S-ABC的外接球的半径，由此可求三棱锥S-ABC的外接球的表面积．

解答解：由题意，SC的中点为球心，∵SA⊥平面ABC，SA=AC=2，
∴SC=2$\sqrt{2}$，
∴球的半径为$\sqrt{2}$，
∴该四面体的外接球的表面积为4π•2=8π．
故答案为：8π．

点评本题考查球的表面积的计算，考查学生分析解决问题的能力，属于基础题．

练习册系列答案

芒果英语阅读理解与完形填空150篇系列答案

相关题目

4．

如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=BC=AC=2，AB=2$\sqrt{2}$，D、E分别是的AB，BB₁的中点．
（Ⅰ）证明：BC₁∥平面A₁CD；
（Ⅱ）求二面角D-A₁C-E的正弦值．

5．在三棱锥P-ABC中，PA⊥平面ABC，PA=2，BC=$\sqrt{2}$，又∠BAC=135°，则该三棱锥外接球的表面积为（　　）

2．（1）已知函数f（x）=|x-1|+|x-3|，g（a）=4a-a²，使不等式f（x）＞g（a）对?a∈R恒成立，求实数x的取值范围；
（2）已知a，b，c∈R⁺，a+b+c=1，求$\sqrt{a}$+$\sqrt{2b}$+$\sqrt{3c}$的最大值．

9．若a＜b＜0，那么下列不等式成立的是（　　）

a²＜b²

2${\;}^{\frac{1}{b}}$＜2${\;}^{\frac{1}{a}}$

19．已知函数f（x）=lnx-2ax，a∈R．
（1）若函数y=f（x）存在与直线2x-y=0平行的切线，求实数a的取值范围；
（2）已知a＞1设g（x）=f（x）+$\frac{1}{2}{x^2}$，若g（x）有极大值点x₁，求证：x₁lnx₁-ax₁²+1＞0．

6．

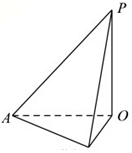如图，有一建筑物OP，为了测量它的高度，在地面上选一长度为40m的基线AB，若在点A处测得P点的仰角为30°，在B点处的仰角为45°，且∠AOB=30°，则建筑物的高度为（　　）

3．已知等差数列{a_n}的前n项和为S_n，且S₆=5S₂+18，a_3n=3a_n，数列{b_n}满足b₁•b₂•…•b_n=4^S_n．
（Ⅰ）求数列{a_n}，{b_n}的通项公式；
（Ⅱ）令c_n=log₂b_n，且数列$\left\{{\frac{1}{{{c_n}•{c_{n+1}}}}}\right\}$的前n项和为T_n，求T₂₀₁₆．

4．数列{a_n}的前n项和记为S_n，a₁=2，a_n+1=S_n+2（n∈N^*）．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）求数列{na_n}的前n项和T_n．

试题分类